
【题目】已知圆C经过M(![]() ,1),N(
,1),N(![]() ,1)两点,且圆心C在直线x+y﹣3=0上,过点A(﹣1,0)的动直线l与圆C相交于P、Q两点.
,1)两点,且圆心C在直线x+y﹣3=0上,过点A(﹣1,0)的动直线l与圆C相交于P、Q两点.
(Ⅰ)求圆C的方程;
(Ⅱ)当|PQ|=4![]() 时,求直线l的方程.
时,求直线l的方程.
科目:高中数学 来源: 题型:
【题目】某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为![]() 和
和![]() ,现安排甲组研发新产品
,现安排甲组研发新产品![]() ,乙组研发新产品
,乙组研发新产品![]() .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品![]() 研发成功,预计企业可获得
研发成功,预计企业可获得![]() 万元,若新产品
万元,若新产品![]() 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润![]() 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】社区服务是高中学生社会实践活动的一个重要内容,汉中某中学随机抽取了100名男生、100名女生,了解他们一年参加社区服务的时间,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:小时)进行统计,得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
(单位:小时)进行统计,得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
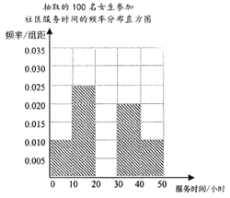
(1)完善男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
抽取的100名男生参加社区服务时间的频率分布表
社区服务时间 | 人数 | 频率 |
| 0.05 | |
| 20 | |
| 0.35 | |
| 30 | |
| ||
合计 | 100 | 1 |
学生社区服务时间合格与性别的列联表
不合格的人数 | 合格的人数 | |
男 | ||
女 |
(2)按高中综合素质评价的要求,高中学生每年参加社区服务的时间不少于20个小时才为合格,根据上面的统计图表,完成抽取的这200名学生参加社区服务时间合格与性别的列联表,并判断是否有![]() 以上的把握认为参加社区服务时间达到合格程度与性别有关,并说明理由.
以上的把握认为参加社区服务时间达到合格程度与性别有关,并说明理由.
(3)用以上这200名学生参加社区服务的时间估计全市9万名高中学生参加社区服务时间的情况,并以频率作为概率.
(i)求全市高中学生参加社区服务时间不少于30个小时的人数.
(ⅱ)对我市高中生参加社区服务的情况进行评价.
参考公式
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.002 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(![]() ,其
,其![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上位于第一象限内的任意一点,
上位于第一象限内的任意一点,![]() 为坐标原点,
为坐标原点,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() ,圆
,圆![]() :
:![]() .
.

(1)求椭圆![]() 和圆
和圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作
作![]() 与圆
与圆![]() 相切于点
相切于点![]() ,使得点
,使得点![]() ,点
,点![]() 在
在![]() 的两侧.求四边形
的两侧.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义向量![]() 的“相伴函数”为
的“相伴函数”为![]() ,函数
,函数![]() 的“相伴向量”为
的“相伴向量”为![]() ,其中O为坐标原点,记平面内所有向量的“相伴函数”构成的集合为S.
,其中O为坐标原点,记平面内所有向量的“相伴函数”构成的集合为S.
(1)设![]() ,求证:
,求证:![]() ;
;
(2)已知![]() 且
且![]() ,求其“相伴向量”的模;
,求其“相伴向量”的模;
(3)已知![]()
![]() 为圆
为圆![]() 上一点,向量
上一点,向量![]() 的“相伴函数”
的“相伴函数”![]() 在
在![]() 处取得最大值,当点M在圆C上运动时,求
处取得最大值,当点M在圆C上运动时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网约车的兴起丰富了民众出行的选择,为民众出行提供便利的同时也解决了很多劳动力的就业问题,据某著名网约车公司“滴滴打车”官网显示,截止目前,该公司已经累计解决退伍军人转业为兼职或专职司机三百多万人次,梁某即为此类网约车司机,据梁某自己统计某一天出车一次的总路程数可能的取值是20、22、24、26、28、![]() ,它们出现的概率依次是
,它们出现的概率依次是![]() 、
、![]() 、
、![]() 、
、![]() 、t、
、t、![]() .
.
(1)求这一天中梁某一次行驶路程X的分布列,并求X的均值和方差;
(2)网约车计费细则如下:起步价为5元,行驶路程不超过![]() 时,租车费为5元,若行驶路程超过
时,租车费为5元,若行驶路程超过![]() ,则按每超出
,则按每超出![]() (不足
(不足![]() 也按
也按![]() 计程)收费3元计费.依据以上条件,计算梁某一天中出车一次收入的均值和方差.
计程)收费3元计费.依据以上条件,计算梁某一天中出车一次收入的均值和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米.

(1)现在准备养一批供游客观赏的鱼,分别在AB、BC、CA上取点D,E,F,如图(1),使得EF‖AB,EF⊥ED,在△DEF喂食,求△DEF 面积S△DEF的最大值;
(2)现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,如图(2),建造△DEF
连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,求△DEF边长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com