
在△ABC中, 分别为内角A,B,C的对边,且
分别为内角A,B,C的对边,且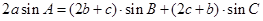
(1)求A的大小;
(2)若 ,试判断△ABC的形状.
,试判断△ABC的形状.
(1)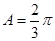 ;(2)
;(2)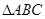 是等腰的钝角三角形.
是等腰的钝角三角形.
解析试题分析:(1)条件中的等式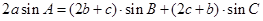 给出了边与角满足的关系,因此可以考虑采用正弦定理实现边角互化,统一转化为边的关系:
给出了边与角满足的关系,因此可以考虑采用正弦定理实现边角互化,统一转化为边的关系: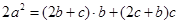 ,
,
即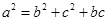 ,再由余弦定理的变式
,再由余弦定理的变式 可知
可知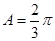 ;(2)由(1)结合条件可知,可将(1)中所得的关系式
;(2)由(1)结合条件可知,可将(1)中所得的关系式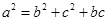 利用正弦定理再转化为角之间的关系:
利用正弦定理再转化为角之间的关系: ,即
,即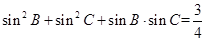 ,再根据条件
,再根据条件 可联立方程组解得
可联立方程组解得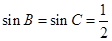 ,结合(1)可知
,结合(1)可知 ,因此
,因此 ,故有
,故有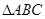 是等腰的钝角三角形.
是等腰的钝角三角形.
试题解析:(1)∵ ,
,
∴根据正弦定理得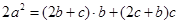 , 2分
, 2分
即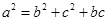 , ∴
, ∴ , 4分
, 4分
又 , ∴
, ∴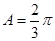 6分
6分
(2)由(1)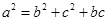 根据正弦定理得
根据正弦定理得 , 8分
, 8分
即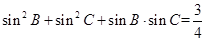 ①,又∵
①,又∵ ②,联立①,②,
②,联立①,②,
得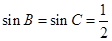 ,.......... 10分
,.......... 10分
又∵ ,∴
,∴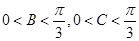 ,∴
,∴ , 11分
, 11分
故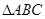 是等腰的钝角三角形. 12分
是等腰的钝角三角形. 12分
考点:正余弦定理相结合解三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com