
【题目】将一枚骰子先后抛掷两次.
(1)一共有多少种不同的结果?
(2)其中向上的数之和是5的结果有多少种?
(3)向上的数之和是5的概率是多少?
【答案】(1)36,(2)见解析(3)![]()
【解析】试题分析:(1)骰子先后抛掷两次,利用列举法求出一共有36种不同的结果.
(2)利用列举法能求出其中向上的点数之和是5的结果有4种.
(3)利用古典概型概率计算公式能求出向上点点数之和为5的概率.
试题解析:
(1)先将骰子抛掷一次,它落地时,向上的数有1,2,3,…,6这6种结果,每种结果又对应着第二次抛掷时的6种可能情况,所以一共有36种不同的结果.
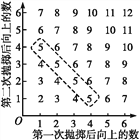
(2)在(1)的所有结果中向上的数之和为5的结果有(1,4),(2,3),(3,2),(4,1)这4种,其中括号内的前后2个数分别为第一、二次抛掷后向上的数,如图所示,其中坐标平面内的数表示相应两次抛掷后向上的数的和.
(3)所有36种结果是等可能出现的,其中向上的数之和是5的结果(记为事件A)有4种,
因此所求概率P(A)=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且 ![]()

(1)求证:不论 ![]() 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量 ![]() 与
与 ![]() 的随机变量
的随机变量 ![]() 越大,说明“
越大,说明“ ![]() 与
与 ![]() 有关系”的可信度越大.
有关系”的可信度越大.
②以模型 ![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设 ![]() ,将其变换后得到线性方程
,将其变换后得到线性方程 ![]() ,则
,则 ![]() 的值分别是
的值分别是 ![]() 和0.3.
和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为 ![]() 中,
中, ![]() ,则
,则 ![]() .
.
④如果两个变量 ![]() 与
与 ![]() 之间不存在着线性关系,那么根据它们的一组数据
之间不存在着线性关系,那么根据它们的一组数据 ![]() 不能写出一个线性方程
不能写出一个线性方程
正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数f(x)中,满足“x1x2∈(0,+∞)且x1≠x2有(x1﹣x2)[f(x1)﹣f(x2)]<0”的是( )
A.f(x)= ![]() ﹣x
﹣x
B.f(x)=x3
C.f(x)=lnx+ex
D.f(x)=﹣x2+2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,在同一个坐标系中,
,在同一个坐标系中,![]() 及
及![]() 的部分图象如图所示,则( ).
的部分图象如图所示,则( ).

A. 当![]() 时,
时,![]() 取得最大值 B. 当
取得最大值 B. 当![]() 时,
时,![]() 取得最大值
取得最大值
C. 当![]() 时,
时,![]() 取得最小值 D. 当
取得最小值 D. 当![]() 时,
时,![]() 取得最小值
取得最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(Ⅰ)求a,b的值;
(Ⅱ)已知f(x)在定义域上为减函数,若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0(k为常数)恒成立.求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,且a2+b2= ![]() ,若a+b≤m恒成立,
,若a+b≤m恒成立,
(Ⅰ)求m的最小值;
(Ⅱ)若2|x﹣1|+|x|≥a+b对任意的a,b恒成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,均值与方差都不变;
②设有一个回归方程 ![]() ,变量x增加一个单位时,y平均增加3个单位;
,变量x增加一个单位时,y平均增加3个单位;
③线性回归方程 ![]() 必经过点
必经过点 ![]() ;
;
④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.其中错误的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com