
【题目】如图,PA⊥平面ABCD,四边形ABCD是矩形,![]() ,
,![]() ,点F为PB中点,点E在边BC上移动.
,点F为PB中点,点E在边BC上移动.

(Ⅰ)求证:PD∥平面AFC;
(Ⅱ)若![]() ,求证:
,求证:![]() ;
;
(Ⅲ)若二面角![]() 的大小为60°,则CE为何值时,三棱锥
的大小为60°,则CE为何值时,三棱锥![]() 的体积为
的体积为![]() .
.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)连接![]() ,设
,设![]() ,底面是矩形,可知
,底面是矩形,可知![]() 是
是![]() 的中点,利用中位线的性质、直线与平面平行的判定定理,可证出PD∥平面AFC;
的中点,利用中位线的性质、直线与平面平行的判定定理,可证出PD∥平面AFC;
(Ⅱ)由![]() ,
,![]() ,点F为PB中点,可知
,点F为PB中点,可知![]() , 由PA⊥平面
, 由PA⊥平面![]() ,可得
,可得![]() ,由四边形
,由四边形![]() 是矩形,可知
是矩形,可知![]() ,这样可以得到
,这样可以得到![]() 平面
平面![]() ,因此可证出
,因此可证出![]() ,这样可以证出
,这样可以证出![]() 平面
平面![]() ,这样就可以证明出
,这样就可以证明出![]() ;
;
(Ⅲ)建立空间直角坐标系,通过若二面角![]() 的大小为60°,可以求出
的大小为60°,可以求出![]() 点的坐标,由三棱锥
点的坐标,由三棱锥![]() 的体积为
的体积为![]() ,可以求出CE的长.
,可以求出CE的长.
(Ⅰ)连接![]() ,设
,设![]() ,如下图所示:
,如下图所示:

四边形ABCD是矩形,所以![]() 是
是![]() 的中点, F为PB中点,所以有
的中点, F为PB中点,所以有![]() ,
,
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,由直线与平面平行的判定定理可知: PD∥平面AFC;
,由直线与平面平行的判定定理可知: PD∥平面AFC;
(Ⅱ)由![]() ,
,![]() ,所以
,所以![]() 是等腰三角形,点F为PB中点,所以有
是等腰三角形,点F为PB中点,所以有![]() , 因为PA⊥平面
, 因为PA⊥平面![]() ,而
,而![]() 平面
平面![]() ,于是有
,于是有![]() ,
,
因为四边形![]() 是矩形,所以
是矩形,所以![]() ,又
,又![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,而
,而![]()
![]() ,
,
所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以 ![]() ;
;
(Ⅲ)建立如上图所示的空间直角坐标系,
设![]() ,,
,,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() 则有
则有
 ,而PA⊥平面
,而PA⊥平面![]() ,所以
,所以![]() 是平面
是平面![]() 的法向量,所以有
的法向量,所以有![]() ,
,
![]() ,设
,设![]() ,
,![]() ,
,
三棱锥![]() 的体积为
的体积为![]() ,
,![]() 解得
解得![]() ,
,
所以当![]() 时,三棱锥
时,三棱锥![]() 的体积为
的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】定义区间![]() ,
,![]() ,
,![]() ,
,![]() 的长度均为
的长度均为![]() ,其中
,其中![]() .
.
(1)已知函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,写出区间
,写出区间![]() 长度的最大值与最小值.
长度的最大值与最小值.
(2)已知函数![]() 的定义域为实数集
的定义域为实数集![]() ,满足
,满足![]() (
(![]() 是
是![]() 的非空真子集).集合
的非空真子集).集合![]() ,
,![]() ,求
,求![]() 的值域所在区间长度的总和.
的值域所在区间长度的总和.
(3)定义函数![]() ,判断函数
,判断函数![]() 在区间
在区间![]() 上是否有零点,并求不等式
上是否有零点,并求不等式![]() 解集区间的长度总和.
解集区间的长度总和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解高中生的艺术素养,从学校随机选取男,女同学各50人进行研究,对这100名学生在音乐、美术、戏剧、舞蹈等多个艺术项目进行多方位的素质测评,并把调查结果转化为个人的素养指标![]() 和
和![]() ,制成下图,其中“*”表示男同学,“+”表示女同学.
,制成下图,其中“*”表示男同学,“+”表示女同学.

若![]() ,则认定该同学为“初级水平”,若
,则认定该同学为“初级水平”,若![]() ,则认定该同学为“中级水平”,若
,则认定该同学为“中级水平”,若![]() ,则认定该同学为“高级水平”;若
,则认定该同学为“高级水平”;若![]() ,则认定该同学为“具备一定艺术发展潜质”,否则为“不具备明显艺术发展潜质”.
,则认定该同学为“具备一定艺术发展潜质”,否则为“不具备明显艺术发展潜质”.
(I)从50名女同学的中随机选出一名,求该同学为“初级水平”的概率;
(Ⅱ)从男同学所有“不具备明显艺术发展潜质的中级或高级水平”中任选2名,求选出的2名均为“高级水平”的概率;
(Ⅲ)试比较这100名同学中,男、女生指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在世界数学史上是一个伟大的创造. 算筹实际上是一根根同样长短的小木棍,用算筹表示数1~9的方法如图:例如:163可表示为“![]() ”,27可表示为“
”,27可表示为“![]() ”.现有6根算筹,用来表示不能被10整除的两位数,算筹必须用完,则这样的两位数的个数为_________.
”.现有6根算筹,用来表示不能被10整除的两位数,算筹必须用完,则这样的两位数的个数为_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
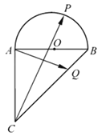
【题目】如图,在等腰直角三角形ABC中,∠CAB=90°,AB=2,以AB为直径在△ABC外作半圆O,P为半圆弧AB上的动点,点Q在斜边BC上,若![]() =
=![]() ,则
,则![]() 的最小值为_______.
的最小值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com