
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若存在常数
,若存在常数![]() ,使得
,使得![]() 对任意的
对任意的![]() 成立,则称函数
成立,则称函数![]() 是“类周期函数”.
是“类周期函数”.
(1)判断函数![]() ,
,![]() 是否是“类周期函数”,并证明你的结论;
是否是“类周期函数”,并证明你的结论;
(2)求证:若函数![]() 是“类周期函数”,且
是“类周期函数”,且![]() 是偶函数,则
是偶函数,则![]() 是周期函数;
是周期函数;
(3)求证:当![]() 时,函数
时,函数![]() 一定是“类周期函数”.
一定是“类周期函数”.
【答案】(1)函数![]() 不是“类周期函数”,
不是“类周期函数”, ![]() 是“类周期函数”,证明见解析(2)证明见解析(3)证明见解析
是“类周期函数”,证明见解析(2)证明见解析(3)证明见解析
【解析】
(1)利用反证法可证断函数![]() 不是“类周期函数”,当
不是“类周期函数”,当![]() 时,利用定义可证
时,利用定义可证![]() 是“类周期函数”;
是“类周期函数”;
(2)根据![]() ,
,![]() ,
,![]() ,可推出
,可推出![]() ,结论得证;
,结论得证;
(3)由![]() ,即
,即![]() ,也就是
,也就是![]() 存在非零实根,可证得结论正确.
存在非零实根,可证得结论正确.
(1)函数![]() 不是“类周期函数”,
不是“类周期函数”, ![]() 是“类周期函数”,
是“类周期函数”,
证明:假设函数![]() 是“类周期函数”,
是“类周期函数”,
则![]() ,即
,即![]() 对任意的
对任意的![]() 成立,
成立,
令![]() 得
得![]() ,所以
,所以![]() ,这与
,这与![]() 相矛盾,故假设不成立,
相矛盾,故假设不成立,
所以函数![]() 不是“类周期函数”;
不是“类周期函数”;
因为![]() 时,
时,![]()
![]() ,根据定义可知
,根据定义可知![]() 是“类周期函数”.
是“类周期函数”.
(2)因为函数![]() 是“类周期函数”,
是“类周期函数”,
所以存在常数![]() ,使得
,使得![]() 对任意的
对任意的![]() 成立,
成立,
所以![]() ,
,
又![]() 为偶函数,所以
为偶函数,所以![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又![]() 为偶函数,所以
为偶函数,所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() 是周期为
是周期为![]() 的周期函数.
的周期函数.
(3)当![]() 时,假设函数
时,假设函数![]() 是“类周期函数”,
是“类周期函数”,
则存在常数![]() ,使得
,使得![]() 对任意的
对任意的![]() 成立,
成立,
即存在常数![]() ,使得
,使得![]() 对任意的
对任意的![]() 成立,
成立,
所以![]() ,此方程有非零实数解,
,此方程有非零实数解,
故当![]() 时,函数
时,函数![]() 一定是“类周期函数”.
一定是“类周期函数”.


科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“美、丽、中、国”四个字,有放回地从中任取一个小球,直到“中”“国”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“中、国、美、丽”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此可以估计,恰好第三次就停止的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,离心率
,离心率![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,圆
为原点,圆![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一动点,若直线
上一动点,若直线![]() 、
、![]() 与
与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
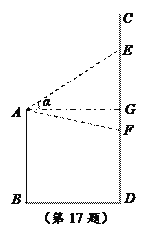
【题目】如图,某企业的两座建筑物AB,CD的高度分别为20m和40m,其底部BD之间距离为20m.为响应创建文明城市号召,进行亮化改造,现欲在建筑物AB的顶部A处安装一投影设备,投影到建筑物CD上形成投影幕墙,既达到亮化目的又可以进行广告宣传.已知投影设备的投影张角∠EAF为![]() ,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
(1)求y关于α的函数关系式![]() ,并求出定义域;
,并求出定义域;
(2)当投影的图像最清晰时,求幕墙EF的高度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除
的包裹,除![]() 收费10元之外,超过
收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() 时按
时按![]() 计算)需再收5元.公司从承揽过的包裹中,随机抽取100件,其重量统计如下:
计算)需再收5元.公司从承揽过的包裹中,随机抽取100件,其重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 | 43 | 30 | 15 | 8 | 4 |
公司又随机抽取了60天的揽件数,得到频数分布表如下:
揽件数 |
|
|
|
|
|
天数 | 6 | 6 | 30 | 12 | 6 |
以记录的60天的揽件数的频率作为各揽件数发生的概率
(1)计算该公司3天中恰有2天揽件数在![]() 的概率;
的概率;
(2)估计该公司对每件包裹收取的快递费的平均值;
(3)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用做其他费用,目前前台有工作人员3人,每人每天揽件不超过150件,每人每天工资100元,公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润有利?
(注:同一组中的揽件数以这组数据所在区间中点值作代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一张半径为3的圆形铁皮中裁剪出一块扇形铁皮(如图1阴影部分),并卷成一个深度为![]() 米的圆锥筒(如图2).若所裁剪的扇形铁皮的圆心角为
米的圆锥筒(如图2).若所裁剪的扇形铁皮的圆心角为![]() .
.
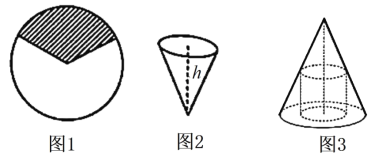
(1)求圆锥筒的容积;
(2)在(1)中的圆锥内有一个底面圆半径为![]() 的内接圆柱(如图3),求内接圆柱侧面积最大时
的内接圆柱(如图3),求内接圆柱侧面积最大时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 在点P(1,
在点P(1,![]() )处的切线方程;
)处的切线方程;
(2)若关于x的不等式![]() 有且仅有三个整数解,求实数t的取值范围;
有且仅有三个整数解,求实数t的取值范围;
(3)若![]() 存在两个正实数
存在两个正实数![]() ,
,![]() 满足
满足![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
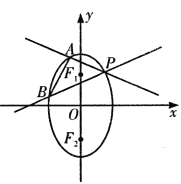
【题目】已知椭圆![]() 两焦点分别为
两焦点分别为![]() 是椭圆在第一象限弧上一点,并满足
是椭圆在第一象限弧上一点,并满足![]() ,过P作倾斜角互补的两条直线
,过P作倾斜角互补的两条直线![]() 分别交椭圆于
分别交椭圆于![]() 两点.
两点.
(1)求![]() 点坐标;
点坐标;
(2)求证:直线![]() 的斜率为定值;
的斜率为定值;
(3)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com