
【题目】已知椭圆![]() :
:![]() 离心率是
离心率是![]() 分别是椭圆
分别是椭圆![]() 的左右焦点,过
的左右焦点,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() ,交椭圆
,交椭圆![]() 于
于![]() ,
,![]() 两点,且三角形
两点,且三角形![]() 周长
周长![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 分别交
分别交![]() 轴于不同的两点
轴于不同的两点![]() ,
,![]() .如果
.如果![]() 为锐角,求
为锐角,求![]() 的取值范围.
的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.![]() 是抛物线
是抛物线![]() 的焦点,过焦点的直线
的焦点,过焦点的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求抛物线![]() 的方程.
的方程.
(2)过点![]() ,
,![]() 作抛物线
作抛物线![]() 的切线
的切线![]() ,
,![]() ,
,![]() 是
是![]() ,
,![]() 的交点,求证:点
的交点,求证:点![]() 在定直线上.
在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是等边三角形,
的底面是等边三角形,![]() 在底面ABC上的射影为△ABC的重心G.
在底面ABC上的射影为△ABC的重心G.
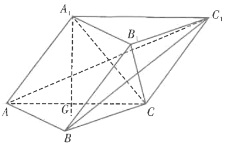
(1)已知![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
(2)已知平面![]() 与平面ABC所成的二面角为60°,G到直线AB的距离为a,求锐二面角
与平面ABC所成的二面角为60°,G到直线AB的距离为a,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过椭圆![]() 的四个顶点与坐标轴垂直的四条直线围成的矩形
的四个顶点与坐标轴垂直的四条直线围成的矩形![]() (
(![]() 是第一象限内的点)的面积为
是第一象限内的点)的面积为![]() ,且过椭圆
,且过椭圆![]() 的右焦点
的右焦点![]() 的倾斜角为
的倾斜角为![]() 的直线过点
的直线过点![]() .
.
(1)求椭圆![]() 的标准方程
的标准方程
(2)若射线![]() 与椭圆
与椭圆![]() 的交点分别为
的交点分别为![]() .当它们的斜率之积为
.当它们的斜率之积为![]() 时,试问
时,试问![]() 的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国剪纸是我国广大劳动人民在生产与生活实践中创造出来的一种平面剪刻艺术.民间剪纸艺术是我国优秀的非物质文化遗产之一,在千百年的发展过程中,积淀了丰厚的文化历史,取得了卓越的艺术成就.2020年3月发行的邮票《中国剪纸(二)》共4枚,第一枚邮票《三娘教子》(如图1)出自“孟母教子”的故事,讲述了母亲通过断织等行为教育孩子努力上进,懂得感恩.图2是某剪纸艺术家根据第一枚邮票用一张半径为4个单位的圆形纸片裁剪而成的《三娘教子》剪纸.为了测算图2中有关部分的面积,在圆形区域内随机投掷400个点,其中落入图案上的点有225个,据此可估计剪去部分纸片的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,点![]() 在曲线
在曲线![]() 上,直线l过点
上,直线l过点![]() 且与OM垂直,垂足为P.
且与OM垂直,垂足为P.
(1)当![]() 时,求在直角坐标系下点
时,求在直角坐标系下点![]() 坐标和l的方程;
坐标和l的方程;
(2)当M在C上运动且P在线段OM上时,求点P在极坐标系下的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com