
【题目】求函数f(x)= ![]() (a>0且a≠1)的值域.
(a>0且a≠1)的值域.
【答案】解:令t=2x﹣x2=﹣(x﹣1)2+1,
则t∈(0,1],
当0<a<1时,f(x)≥loga1=0
当a>1时,f(x)≤loga1=0
故当0<a<1时,f(x)的值域为[0,+∞),
当a>1时,f(x)的值域为(﹣∞,0]
【解析】令t=2x﹣x2=﹣(x﹣1)2+1,t∈(0,1],进行换元,当0<a<1时,f(x)≥loga1=0,当a>1时,f(x)≤loga1=0,从而得出f(x)的值域.
【考点精析】解答此题的关键在于理解函数的值域的相关知识,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,以及对复合函数单调性的判断方法的理解,了解复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】将2张边长均为1分米的正方形纸片分别按甲、乙两种方式剪裁并废弃阴影部分.
(1)在图甲的方式下,剩余部分恰能完全覆盖某圆锥的表面,求该圆锥的母线长及底面半径;
(2)在图乙的方式下,剩余部分能完全覆盖一个长方体的表面,求长方体体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数λ>0,设函数f(x)=eλx﹣ ![]() .
.
(Ⅰ)当λ=1时,求函数g(x)=f(x)+lnx﹣x的极值;
(Ⅱ)若对任意x∈(0,+∞),不等式f(x)≥0恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数满足:f(x+4)=f(x)+f(2),且当x∈[0,2]时,y=f(x)单调递减,给出以下四个命题:
①f(2)=0;
②x=﹣4为函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[8,10]单调递增;
④若方程f(x)=m在[﹣6,﹣2]上的两根为x1 , x2 , 则x1+x2=﹣8.
上述命题中所有正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C满足sin2A+sin(A﹣B+C)=sin(C﹣A﹣B)+ ![]() ,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
A.bc(b+c)>8
B.ab(a+b)>16 ![]()
C.6≤abc≤12
D.12≤abc≤24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的右焦点为F2(1,0),点H(2,
=1(a>b>0)的右焦点为F2(1,0),点H(2, ![]() )在椭圆上.
)在椭圆上.
(1)求椭圆的方程;
(2)点M在圆x2+y2=b2上,且M在第一象限,过M作圆x2+y2=b2的切线交椭圆于P,Q两点,求证:△PF2Q的周长是定值.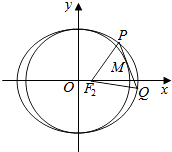
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.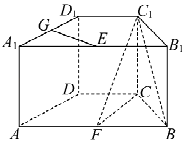
(Ⅰ)求证:GE⊥平面FCC1;
(Ⅱ)求二面角B﹣FC1﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com