
(13分)(2011•湖北)设函数f(x)=x3+2ax2+bx+a,g(x)=x2﹣3x+2,其中x∈R,a、b为常数,已知曲线y=f(x)与y=g(x)在点(2,0)处有相同的切线l.
(Ⅰ) 求a、b的值,并写出切线l的方程;
(Ⅱ)若方程f(x)+g(x)=mx有三个互不相同的实根0、x1、x2,其中x1<x2,且对任意的x∈[x1,x2],f(x)+g(x)<m(x﹣1)恒成立,求实数m的取值范围.
(Ⅰ)x﹣y﹣2=0(Ⅱ)(﹣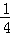 ,0)
,0)
解析试题分析:(I) 利用曲线y=f(x)与y=g(x)在点(2,0)处有相同的切线l,可得f(2)=g(2)=0,f'(2)=g'(2)=1.即为关于a、b的方程,解方程即可.
(II)把方程f(x)+g(x)=mx有三个互不相同的实根转化为x1,x2是x2﹣3x+2﹣m=0的两相异实根.求出实数m的取值范围以及x1,x2与实数m的关系,再把f(x)+g(x)<m(x﹣1)恒成立问题转化为求函数f(x)+g(x)﹣mx在x∈[x1,x2]上的最大值,综合在一起即可求出实数m的取值范围.
解:(I) f'(x)=3x2+4ax+b,g'(x)=2x﹣3.
由于曲线y=f(x)与y=g(x)在点(2,0)处有相同的切线l.
故有f(2)=g(2)=0,f'(2)=g'(2)=1.
由此得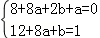 ,解得
,解得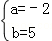 ,
,
所以a=﹣2,b=5..切线的方程为x﹣y﹣2=0.
(II)由(I)得f(x)=x3﹣4x2+5x﹣2,所以f(x)+g(x)=x3﹣3x2+2x.
依题意,方程x(x2﹣3x+2﹣m)=0,有三个互不相等的实根0,x1,x2,
故x1,x2是x2﹣3x+2﹣m=0的两相异实根.
所以△=9﹣4(2﹣m)>0,解得m>﹣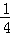 .
.
又对任意的x∈[x1,x2],f(x)+g(x)<m(x﹣1)恒成立,
特别地取x=x1时,f(x1)+g(x1)<m(x1﹣1)成立,得m<0.
由韦达定理得x1+x2=3>0,x1x2=2﹣m>0.故0<x1<x2.
对任意的x∈[x1,x2],x﹣x2≤0,x﹣x1≥0,x>0.
则f(x)+g(x)﹣mx=x(x﹣x1)(x﹣x2)≤0,又f(x1)+g(x1)﹣mx1=0.
所以f(x)+g(x)﹣mx在x∈[x1,x2]上的最大值为0.
于是当m<0,对任意的x∈[x1,x2],f(x)+g(x)<m(x﹣1)恒成立,
综上得:实数m的取值范围是(﹣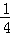 ,0).
,0).
点评:本题主要考查函数,导数,不等式等基础知识,同时考查综合运用数学知识进行推理论证的能立,以及函数与方程和特殊与一般的思想.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:解答题
某小区想利用一矩形空地 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
, ,且
,且 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一直线交
作一直线交 于
于 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设 .
.
(1)将五边形 的面积
的面积 表示为
表示为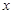 的函数;
的函数;
(2)当 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
定义函数 (
( 为定义域)图像上的点到坐标原点的距离为函数的
为定义域)图像上的点到坐标原点的距离为函数的 的模.若模存在最大值,则称之为函数
的模.若模存在最大值,则称之为函数 的长距;若模存在最小值,则称之为函数
的长距;若模存在最小值,则称之为函数 的短距.
的短距.
(1)分别判断函数 与
与 是否存在长距与短距,若存在,请求出;
是否存在长距与短距,若存在,请求出;
(2)求证:指数函数 的短距小于1;
的短距小于1;
(3)对于任意 是否存在实数
是否存在实数 ,使得函数
,使得函数 的短距不小于2,若存在,请求出
的短距不小于2,若存在,请求出 的取值范围;不存在,则说明理由?
的取值范围;不存在,则说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,把边长为10的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设其高为h,体积为V(不计接缝).
(1)求出体积V与高h的函数关系式并指出其定义域;
(2)问当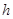 为多少时,体积V最大?最大值是多少?
为多少时,体积V最大?最大值是多少?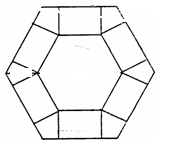
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如果函数 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意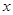 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。
(1)判断函数 是否具有“
是否具有“ 性质”,若具有“
性质”,若具有“ 性质”,求出所有
性质”,求出所有 的值;若不具有“
的值;若不具有“ 性质”,说明理由;
性质”,说明理由;
(2)已知 具有“
具有“ 性质”,且当
性质”,且当 时
时 ,求
,求 在
在 上有最大值;
上有最大值;
(3)设函数 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若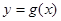 与
与 交点个数为2013,求
交点个数为2013,求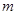 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com