
分析 (1)根据向量的坐标运算和数量积,得到5x2-20x+12,利用二次函数的性质求出x的值,问题得以解决,
(2)根据cos∠AMB=$\frac{\overrightarrow{MA}•\overrightarrow{MB}}{|\overrightarrow{MA}||\overrightarrow{MB}|}$,即可求出答案.
解答 解:(1)∵$\overrightarrow{OA}$=(1,7),$\overrightarrow{OB}$=(5,1),点M(2x,x),
∴$\overrightarrow{MA}$=(1-2x,7-x),$\overrightarrow{MB}$=(5-2x,1-x),
∴$\overrightarrow{MA}$$•\overrightarrow{MB}$=(1-2x)(5-2x)+(7-x)(1-x)=5x2-20x+12=5(x-2)2-8
当x=2时,$\overrightarrow{MA}$$•\overrightarrow{MB}$取最小值,
∴$\overrightarrow{OM}$的坐标为(4,2),
(2)由(1),得$\overrightarrow{MA}$=(-3,5),$\overrightarrow{MB}$=(1,-1),
∴|$\overrightarrow{MA}$|=$\sqrt{34}$,|$\overrightarrow{MB}$|=$\sqrt{2}$,$\overrightarrow{MA}$•$\overrightarrow{MB}$=-8,
∴cos∠AMB=$\frac{\overrightarrow{MA}•\overrightarrow{MB}}{|\overrightarrow{MA}||\overrightarrow{MB}|}$=$\frac{-8}{\sqrt{34}•\sqrt{2}}$=-$\frac{4\sqrt{17}}{17}$.
点评 本题考查了向量的坐标运算和函数最值问题,以及数量积定义的应用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
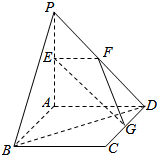 平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=PD=2,E,F,G分别是线段PA,PD,CD的中点
平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=PD=2,E,F,G分别是线段PA,PD,CD的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com