解:(1)∵f(x)=log
4(4
x+1)+kx(k∈R)是偶函数.
∴f(-x)=f(x)
即log
4(4
-x+1)-kx=log
4(4
x+1)+kx
即log
4(4
x+1)-(k+1)x=log
4(4
x+1)+kx
即2k+1=0
∴k=

证明:(2)由(1)得f(x)=log
4(4
x+1)

x
令y=log
4(4
x+1)-x
由于y=log
4(4
x+1)-x为减函数,且恒为正
故当b>0时,y=log
4(4
x+1)-x-b有唯一的零点,此时函数y=f(x)的图象与直线
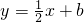
有一个交点,
当b≤0时,y=log
4(4
x+1)-x-b没有零点,此时函数y=f(x)的图象与直线
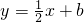
没有交点
分析:(1)根据偶函数的定义可知f(-x)=f(x),然后化简可得2k+1=0,可求出k的值;
(2)令y=log
4(4
x+1)-x,由于y=log
4(4
x+1)-x为减函数,且恒为正,当b>0时,y=log
4(4
x+1)-x-b有唯一的零点,当b≤0时,y=log
4(4
x+1)-x-b没有零点.
点评:本题主要考查了函数的奇偶性,以及函数零点的判定定理,属于中档题.

 x+b的零点的个数.
x+b的零点的个数.
 x
x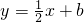 有一个交点,
有一个交点,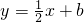 没有交点
没有交点

 优加精卷系列答案
优加精卷系列答案