
分析 (1)根据题意,由于函数f(x)是定义在R上的奇函数,则有f(0)=0,f(1)=-f(-1),代入数据,计算可得a、b的值;
(2)首先对f(x)的表达式变形可得f(x)=1-$\frac{2}{{2}^{x}+1}$,用作差法判断函数单调性即可.
解答 解:(1)∵f(x)=$\frac{{2}^{x}-a}{{2}^{x}+b}$定义在R上的奇函数,
则有f(0)=0,即$\frac{1-a}{1+b}$=0,解可得a=1;
又f(1)=-f(-1),即$\frac{2-a}{2+b}$=-$\frac{\frac{1}{2}-1}{\frac{1}{2}+b}$,解可得b=1.
∴f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$;
(2)由(1)可得,f(x)=1-$\frac{2}{{2}^{x}+1}$
设x1<x2,
则f(x1)-f(x2)=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$,
∵x1<x2,
∴${2}^{{x}_{1}}-{2}^{{x}_{2}}$<0,
∴f(x1)-f(x2)<0,
∴f(x)是增函数.
点评 本题考查函数的单调性、奇偶性,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:解答题
数列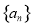 满足:①
满足:①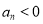 ;②
;②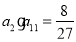 ;③
;③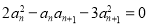 .
.
(1)求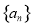 的通项公式;
的通项公式;
(2)设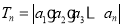 ,问:是否存在常数
,问:是否存在常数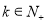 ,使得
,使得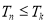 对于任意
对于任意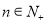 恒成立?若存在,请求出
恒成立?若存在,请求出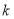 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>c>a | B. | a>c>b | C. | a>b>c | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com