从2,4中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为( )
A.6
B.12
C.18
D.24
【答案】
分析:法一:本题是从两个偶数中任选一个,三个奇数中任选两个共三个数字组成的无重复数字的三位奇数问题,解答时先找出总的选法情况,然后分析得到每一种选法对应6种不同的排列,其中有4个是奇数,2个偶数,则六种选法对应24个不同的奇数;
法二:直接运用分步计数原理,先从2,4中选一个数字,从1,3,5中选两个数字,然后把三个不同的数字安排在三个不同的位置上,要求个位上只能排奇数.
解答:解:法一
从2,4中选一个数字,从1,3,5中选两个数字,选法种数共有(2,1,3),(2,1,5),(2,3,5),
(4,1,3),(4,1,5),(4,3,5)六种,每一种选法可排列组成
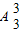
=6个无重复数字的三位数,其中奇数的个数
有4个,故六种选法组成的无重复数字的三位奇数共有4×6=24个.
故选D.
法二
从2,4中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位奇数,可运用分步计数原理解决.
首先从2,4中选一个偶数有
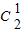
种方法;然后从1,3,5中选两个奇数有
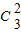
种选法;再把选出的两个奇数任选一个放在三位数的个位位置上有
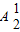
种方法,剩余的一个奇数和选出的一个偶数在十位和百位位置上排列有
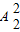
种方法,
由分步计数原理可得,从2,4中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,
其中奇数的个数为
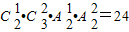
个.
故选D.
点评:本题考查了排列、组合及简单的计数问题,考查了有条件限制排列,解答排列问题时要正确区分有重复排列和无重复排列,关键是做到不重不漏,此题是中低档题.

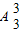 =6个无重复数字的三位数,其中奇数的个数
=6个无重复数字的三位数,其中奇数的个数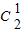 种方法;然后从1,3,5中选两个奇数有
种方法;然后从1,3,5中选两个奇数有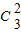 种选法;再把选出的两个奇数任选一个放在三位数的个位位置上有
种选法;再把选出的两个奇数任选一个放在三位数的个位位置上有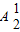 种方法,剩余的一个奇数和选出的一个偶数在十位和百位位置上排列有
种方法,剩余的一个奇数和选出的一个偶数在十位和百位位置上排列有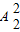 种方法,
种方法,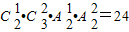 个.
个.
