
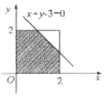
 如图,正方形边长是2,直线x+y-3=0与正方形交于两点,向正方形内投飞镖,则飞镖落在阴影部分内的概率是$\frac{7}{8}$.
如图,正方形边长是2,直线x+y-3=0与正方形交于两点,向正方形内投飞镖,则飞镖落在阴影部分内的概率是$\frac{7}{8}$. 分析 根据几何概率的求法,可以得出镖落在阴影部分的概率就是阴影区域的面积与总面积的比值.
解答 解:观察这个图可知:阴影部分是正方形去掉一个小三角形,
设直线与正方形的两个交点为A,B,
∴在直线AB的方程为x+y-3=0中,
令x=2得A(2,1),
令y=2得B(1,2).
∴三角形ABC的面积为s=$\frac{1}{2}×1×1$=$\frac{1}{2}$,
则飞镖落在阴影部分的概率是:
P=1-$\frac{s}{{s}_{正方形}}$=1-$\frac{\frac{1}{2}}{4}$=1-$\frac{1}{8}$=$\frac{7}{8}$.
故答案为:$\frac{7}{8}$.
点评 本题考查几何概型的概念,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小值4 | B. | 最大值4 | C. | 最小值2 | D. | 最大值2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,3] | B. | [-3,1] | C. | (-∞,-3]∪[1,+∞] | D. | (-∞,1]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{13}{6}$ | C. | $\frac{10}{3}$ | D. | $\frac{17}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com