
已知,函数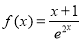 .
.
(1)如果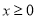 时,
时,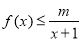 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(2)当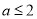 时,求证:
时,求证: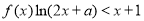 .
.
(1)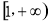 ,(2)详见解析.
,(2)详见解析.
【解析】
试题分析:(1)转化为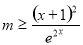 恒成立,求
恒成立,求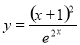 的最大值;通过导数确定函数的单调性,利用单调性求出函数的最大值,
的最大值;通过导数确定函数的单调性,利用单调性求出函数的最大值,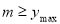 ;令
;令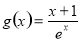 ,通过求其导数,通过导数的正负,判定函数的单调性,从而求出其最大值;
,通过求其导数,通过导数的正负,判定函数的单调性,从而求出其最大值;
(2)首先利用分析法将所要证不等式,逐步分析,找到证明其成立的充分条件,即 ,设函数
,设函数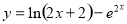 ,利用导数找到其最小值,证明其最小值也大于0,则不等式成立.中档偏难.
,利用导数找到其最小值,证明其最小值也大于0,则不等式成立.中档偏难.
试题解析:(1)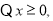
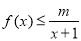 ,
,
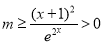 ,
,
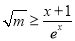 .
.
令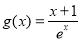 (
(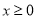 ),
),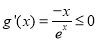 ,
,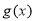 递减,
递减,
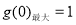 ,∴m的取值范围是
,∴m的取值范围是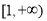 . 5分
. 5分
(2)证明:当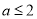 时,
时, 的定义域
的定义域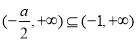 ,
,
∴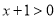 ,要证
,要证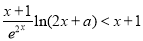 ,只需证
,只需证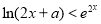
又∵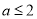 ,∴只需证
,∴只需证 , 8分
, 8分
即证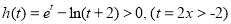
∵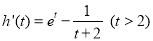 递增,
递增,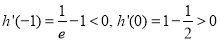 ,
,
∴必有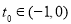 ,使
,使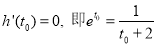 ,即
,即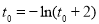 ,
,
且在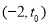 上,
上,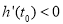 ;在
;在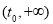 上,
上,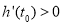 ,
,
∴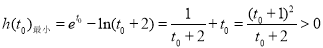
∴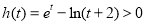 ,即
,即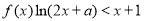 12分
12分
考点:1.函数恒成立问题;2.证明不等式的方法;3.利用导数求函数的最小值.


科目:高中数学 来源:2013-2014学年河南中原名校高三下学期第二次联考理科数学试卷(解析版) 题型:解答题
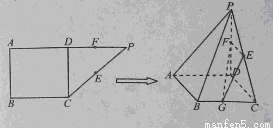
如图,在直角梯形ABCP中,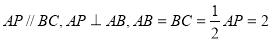 ,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP
,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP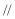 平面EFG;(2)当二面角G-EF-D的大小为
平面EFG;(2)当二面角G-EF-D的大小为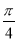 时,求FG与平面PBC所成角的余弦值.
时,求FG与平面PBC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省邯郸市高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
已知 是椭圆
是椭圆 ,
,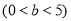 上除顶点外的一点,
上除顶点外的一点, 是椭圆的左焦点,若
是椭圆的左焦点,若 则点
则点 到该椭圆左焦点的距离为( )
到该椭圆左焦点的距离为( )
A.  B.
B.  C .
C . D.
D. 
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省邯郸市高三第一次模拟考试文科数学试卷(解析版) 题型:填空题
已知 是定义在[-1,1]上的奇函数且
是定义在[-1,1]上的奇函数且 ,当
,当 ,且
,且 时,有
时,有 ,若
,若 对所有
对所有 、
、 恒成立,则实数
恒成立,则实数 的取值范围是_________.
的取值范围是_________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
在平面直角坐标系中,曲线C1的参数方程为 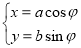 (a>b>0,
(a>b>0,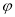 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M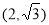 对应的参数
对应的参数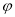 =
= ,
, 与曲线C2交于点D
与曲线C2交于点D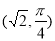
(1)求曲线C1,C2的方程;
(2)A(ρ1,θ),Β(ρ2,θ+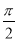 )是曲线C1上的两点,求
)是曲线C1上的两点,求 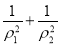 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com