
【题目】在平面直角坐标系中,以坐标原点为中心,以坐标轴为对称轴的帮圆C经过点M(2,1),N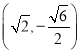 .
.
(1)求椭圆C的标准方程;
(2)经过点M作倾斜角互补的两条直线,分别与椭圆C相交于异于M点的A,B两点,当△AMB面积取得最大值时,求直线AB的方程.
【答案】(1)![]()
(2)![]() 或
或![]()
【解析】
(1)设椭圆C的方程为![]() (
(![]() ,
,![]() ,
,![]() ).
).
根据椭圆过![]() 两点,代入得到方程组,解得.
两点,代入得到方程组,解得.
(2)由直线AM,BM,AB的斜率存在,故.设它们的斜率分别为![]() ,
,![]() ,k.
,k.
设![]() ,
,![]() ,直线AB的方程为
,直线AB的方程为![]() .联立直线与椭圆方程,消元列出韦达定理,由
.联立直线与椭圆方程,消元列出韦达定理,由![]() .即
.即![]() . 即可解得
. 即可解得![]() ,或
,或![]() .分别代入检验,再用弦长公式及点到直线的距离公式,表示出三角形的面积,利用基本不等式求最值.
.分别代入检验,再用弦长公式及点到直线的距离公式,表示出三角形的面积,利用基本不等式求最值.
解:(1)设椭圆C的方程为![]() (
(![]() ,
,![]() ,
,![]() ).
).
∵点![]() 和N
和N 在椭圆C上,
在椭圆C上,
∴ .解得
.解得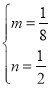 .
.
∴椭圆C的标准方程为![]() .
.
(2)∵点A,B为椭圆上异于M的两点,且直线AM,BM的倾斜角互补,
![]() ,
,![]() ,k.
,k.
设![]() ,
,![]() ,直线AB的方程为
,直线AB的方程为![]() .
.
∴![]() .
.
∴![]() .
.
由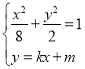 ,消去y,得
,消去y,得![]() .
.
由![]() ,得
,得![]() .
.
∴![]() ,
,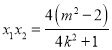 .
.
∴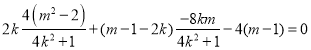 .
.
∴![]() .
.
∴![]() .
.
∴![]() ,或
,或![]() .
.
∵点A,B为椭圆上异于M的两点,
∴当![]() 时,直线AB的方程为
时,直线AB的方程为![]() ,不合题意,舍去.
,不合题意,舍去.
∴直线AB的斜率为![]() .
.
∵![]() ,点M到直线AB的距离为
,点M到直线AB的距离为![]() ,
,
∴![]() 的面积为
的面积为![]() .
.
当且仅当![]() 时,
时,![]() 的面积取得最大值,此时
的面积取得最大值,此时![]() .
.
∵![]() ,
,![]() 满足
满足![]() .
.
∴直线AB的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】 某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上,每隔30分钟抽一包产品,称其重量是否合格,分别记录抽查数据如下(单位:千克):
甲车间:102,101,99,98,103,98,99.
乙车间:110,115,90,85,75,115,110.
(1)这种抽样方式是何种抽样方法;
(2)试根据这组数据说明哪个车间产品较稳定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学文化的优秀遗产,数学家刘徽在注解《九章算术》时,发现当圆内接正多边行的边数无限增加时,多边形的面积可无限逼近圆的面积,为此他创立了割圆术,利用割圆术,刘徽得到了圆周率精确到小数点后四位3.1416,后人称3.14为徽率,如图是利用刘徽的割圆术设计的程序框图,若结束程序时,则输出的![]() 为( )(
为( )(![]() ,
,![]() ,
,![]() )
)
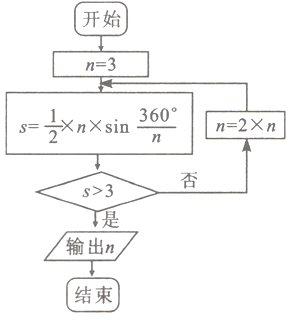
A. 6 B. 12 C. 24 D. 48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在[e,+∞)上的函数f(x)满足f(x)+xlnxf′(x)<0且f(2018)=0,其中f′(x)是函数![]() 的导函数,e是自然对数的底数,则不等式f(x)>0的解集为( )
的导函数,e是自然对数的底数,则不等式f(x)>0的解集为( )
A. [e,2018) B. [2018,+∞) C. (e,+∞) D. [e,e+1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的偶函数f(x)满足对x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣loga(|x|+1)至少有6个零点,则a的取值范围是( )
A.(0,![]() )B.(0,
)B.(0,![]() )C.(0,
)C.(0,![]() )D.(0,
)D.(0,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AB=AC,∠ACB的平分线与AB交于点D,过△ABC的外心O作CD的垂线与AC交于点E,过E作AB的平行线与CD交于点F。证明:

(1)C、E、0、F四点共圆;
(2)A、0、F三点共线;
(3)EA=EF。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com