
【题目】.如图,在三棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD,则下列结论中不一定成立的是 ( )
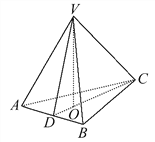
A. AC=BC
B. VC⊥VD
C. AB⊥VC
D. S△VCD·AB=S△ABC·VO
【答案】B
【解析】因为VA=VB,AD=BD,
所以VD⊥AB.因为VO⊥平面ABC,
AB平面ABC,所以VO⊥AB.
又VO∩VD=V,VO平面VCD,VD平面VCD,
所以AB⊥平面VCD,
又CD平面VCD,VC平面VCD,
所以AB⊥VC,AB⊥CD.
又AD=BD,所以AC=BC(线段垂直平分线的性质),因为VO⊥平面ABC,
所以VV-ABC=![]() S△ABC·VO.
S△ABC·VO.
因为AB⊥平面VCD,
所以VV-ABC=VB-VCD+VA-VCD
=![]() S△VCD·BD+
S△VCD·BD+![]() S△VCD·AD
S△VCD·AD
=![]() S△VCD·(BD+AD)
S△VCD·(BD+AD)
=![]() S△VCD·AB,
S△VCD·AB,
所以![]() S△ABC·VO=
S△ABC·VO=![]() S△VCD·AB,
S△VCD·AB,
即S△VCD·AB=S△ABC·VO.综上知,A,C,D正确.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】“菊花”型烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂.通过研究,发现该型烟花爆裂时距地面的高度![]() (单位:米)与时间
(单位:米)与时间![]() (单位:秒)存在函数关系,并得到相关数据如表:
(单位:秒)存在函数关系,并得到相关数据如表:
时间 | 1 |
|
|
高度 |
|
|
|
(1)根据表中数据,从下列函数中选取一个函数描述该型烟花爆裂时距地面的高度![]() 与时间
与时间![]() 的变化关系:
的变化关系: ![]() ,
, ![]() ,
, ![]() ,确定此函数解析式并简单说明理由;
,确定此函数解析式并简单说明理由;
(2)利用你选取的函数,判断烟花爆裂的最佳时刻,并求此时烟花距地面的高度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .

(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且
,且![]() 的离心率为
的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的顶点
的顶点![]() 作两条互相垂直的直线与椭圆分别相交于
作两条互相垂直的直线与椭圆分别相交于![]() 两点.若
两点.若![]() 的角平分线方程为
的角平分线方程为![]() ,求
,求![]() 的面积及直线
的面积及直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球3次均未命中的概率为
,且乙投球3次均未命中的概率为![]() ,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com