
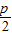 于点M,当|FD|=2时,∠AFD=60°.
于点M,当|FD|=2时,∠AFD=60°.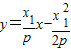 ,所以D(
,所以D(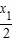 ,0),Q(0,-y1)
,0),Q(0,-y1) ,|FA|=
,|FA|=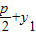 ,∴|FQ|=|FA|,∴△AFQ为等腰三角形,且D为AQ的中点
,∴|FQ|=|FA|,∴△AFQ为等腰三角形,且D为AQ的中点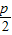 =1
=1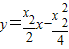 ,与
,与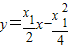 联立,可得P(
联立,可得P(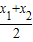 ,
,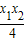 )
)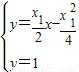 ,可得M(
,可得M( ,1)
,1)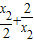 ,1),所以面积S=
,1),所以面积S= [(
[( )-(
)-(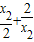 )](1-
)](1-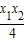 )=
)=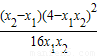 …①
…①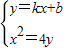 ,消去y可得x2-4kx-4b=0,得x1+x2=4k,x1x2=-4b代入①得:
,消去y可得x2-4kx-4b=0,得x1+x2=4k,x1x2=-4b代入①得: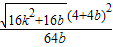 =
=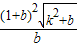 ,要使面积最小,则k=0得到S=
,要使面积最小,则k=0得到S=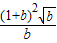 ②
② ,②得S(t)=
,②得S(t)=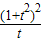 =
=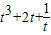 ,S′(t)=
,S′(t)=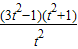 ,
,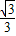 )时,S(t)单调递减;当t∈(
)时,S(t)单调递减;当t∈(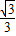 ,+∞)时,S(t)单调递增,
,+∞)时,S(t)单调递增,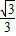 时,S取到最小值为
时,S取到最小值为 ,此时
,此时 ,k=0,
,k=0,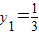 ,
,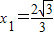 .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| AF |
| FB |
| AB |
| FQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
|
|
|
| ||
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com