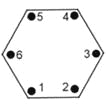
【题目】工人在安装一个正六边形零件时，需要固定如图所示的六个位置的螺丝，第一阶段，首先随意拧一个螺丝，接着拧它对角线上（距离它最远的，下同）螺丝，再随意拧第三个螺丝，第四个也拧它对角线上螺丝，第五个和第六个以此类推，但每个螺丝都不要拧死;第二阶段，将每个螺丝拧死，但不能连续拧相邻的2个螺丝．则不同的固定方式有________．
科目：高中数学 来源： 题型：
【题目】某大学的
名同学准备拼车去旅游，其中大一、大二、大三、大四每个年级各两名，分乘甲、乙两辆汽车.每车限坐
名同学(乘同一辆车的名同学不考虑位置)，其中大一的孪生姐妹需乘同一辆车，则乘坐甲车的名同学中恰有
名同学是来自于同一年级的乘坐方式共有_______种（有数字作答）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一块耕地上种植一种作物，每季种植成本为1000元，此作物的市场价格和这块地上的产量均具有随机性，且互不影响，其具体情况如下表：
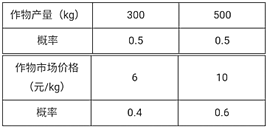
（1）设
表示在这块地上种植1季此作物的利润，求的分布列；
（2）若在这块地上连续3季种植此作物，求这3季中至少有2季的利润不少于2000元的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在含有
个元素的集合
中，若这个元素的一个排列（
，
，…，
）满足
，则称这个排列为集合
的一个错位排列（例如：对于集合
，排列
是
的一个错位排列；排列
不是的一个错位排列）.记集合的所有错位排列的个数为
.
（1）直接写出
，
，
，
的值；
（2）当
时，试用
，
表示，并说明理由；
（3）试用数学归纳法证明：
为奇数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知焦点在
轴上的椭圆
上的点到两个焦点的距离和为10，椭圆经过点
.
（1）求椭圆的标准方程；
（2）过椭圆的右焦点
作与轴垂直的直线
，直线上存在
、
两点满足
，求△
面积的最小值；
（3）若与轴不垂直的直线
交椭圆于
、
两点，交轴于定点，线段
的垂直平分线交轴于点，且
为定值，求点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设甲、乙两位同学上学期间，每天7:10之前到校的概率均为
.假定甲、乙两位同学到校情况互不影响，且任一同学每天到校情况相互独立.
（1）用
表示甲同学上学期间的每周五天中7:10之前到校的天数，求随机变量的分布列和数学期望；
（2）记“上学期间的某周的五天中，甲同学在7:10之前到校的天数比乙同学在7:10之前到校的天数恰好多3天”为事件
，求事件发生的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在极坐标系中，曲线C1，C2的极坐标方程分别为ρ＝－2cosθ，ρcos
＝1.
（1）求曲线C1和C2的公共点的个数；
（2）过极点作动直线与曲线C2相交于点Q，在OQ上取一点P，使|OP|·|OQ|＝2，求点P的轨迹，并指出轨迹是什么图形.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，M是椭圆C的上顶点，
，F2是椭圆C的焦点，
的周长是6．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过动点P（1，t）作直线交椭圆C于A，B两点，且|PA|=|PB|，过P作直线l，使l与直线AB垂直，证明：直线l恒过定点，并求此定点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
