
分析 (1)先求出圆心坐标,可得圆的方程,再设出切线方程,利用点到直线的距离公式,即可求得切线方程;
(2)设出点C,P的坐标,利用|PA|=|2PO|,寻找坐标之间的关系,进一步将问题转化为圆与圆的位置关系,即可得出结论.
解答 解:(1)由题设知,圆心C(a,2a-4)在直x-y-3=0上,解得点C(1,-2)
所以 圆C的方程为(x-1)2+(y+2)2=1…(2分)
①若切线的斜率不存在,则切线方程x=0,符合题意…(4分)
②若切线斜率存在,设切线的方程为y-3=k(x-0),即kx-y+3=0.
由题意知,圆心C(1,-2)到切线kx-y+3=0的距离等于半径1,
即:$\frac{{|{k+2+3}|}}{{\sqrt{1+{k^2}}}}=1$解之得$k=-\frac{12}{5}$,所以切线方程为12x+5y-15=0…(6分)
综上所述,所求切线的方程是x=0或 12x+5y-15=0…(7分)
(2)∵圆心C(a,2a-4),半径为1,所以圆C的方程为(x-a)2+(y-2a+4)2=1.
设点P(x0,y0),因为|PA|=2|PO|∴${x_0}^2+{({y_o}-3)^2}=4({x_0}^2+{y_0}^2)$
化简得${x_0}^2+{({y_0}^2+1)^2}=4$,又因为${({x_0}-a)^2}+{({y_0}-2a+4)^2}=1$…(9分)
所以点P既在以D(0,-1)为圆心,2为半径的圆上.
又在圆C上,即圆C与圆D有公共点P
则1≤CD≤3即$1≤\sqrt{{a^2}+{{(2a-3)}^2}}≤3$
∴$\left\{{\begin{array}{l}{5{a^2}-12a≤0}\\{5{a^2}-12a+8≥0}\end{array}}\right.$
由5a2-12a≤0,且a>0得$0<a≤\frac{12}{5}$
由5a2-12a+8≥0,得a∈R;
所以圆心C的横坐标a的取值范围为$({0,\frac{12}{5}}]$….(12分)
点评 本题考查直线与圆的位置关系,考查圆与圆的位置关系,考查学生的计算能力,考查分类讨论的数学思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在圆上 | B. | 在圆内 | C. | 在圆外 | D. | 以上皆有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
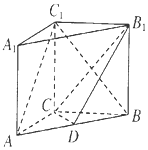 如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com