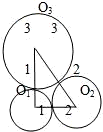Question

半径为1、2、3的三个圆两两外切．证明：以这三个圆的圆心为顶点的三角形是直角三角形．

Answer 1

证明：设⊙O₁、⊙O₂、⊙O₃的半径分别为1、2、3．
因这三个圆两两外切，
故有O₁O₂=1+2=3，O₂O₃=2+3=5，O₁O₃=1+3=4，
则有O₁O₂²+O₁O₃²=3²+4²=5²=O₂O₃²
根据勾股定理的逆定理，
得到△O₁O₂O₃为直角三角形．
分析：根据两圆外切时两圆心之间的距离等于两半径之和，由三个圆的半径分别求出三角形的三边，求出最长一边的平方且求出其余两边的平方和，发现其相等，利用勾股定理的逆定理即可得证．
点评：此题考查学生掌握两圆外切时圆心距与两半径之间的关系，是一道基础题．通过此题，学生要明白判断一个三角形是直角三角形的方法不仅可以根据一个角是直角得到三角形为直角三角形，还可以利用勾股定理的逆定理来判断一个三角形为直角三角形．