
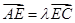 。又以A、B为焦点的双曲线过C、D、E三点。若
。又以A、B为焦点的双曲线过C、D、E三点。若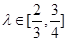 ,则双曲线离心率e的取值范围为( )
,则双曲线离心率e的取值范围为( )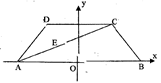
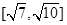 B.
B.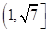 C.
C. D.
D.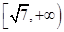
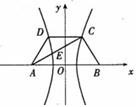
 ,h),E(x0,y0),
,h),E(x0,y0), =
= ,γ0=
,γ0= .
. -
-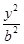 =1,则离心率 e=
=1,则离心率 e= ,
, 代入双曲线的方程,得
代入双曲线的方程,得 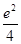 -
- =1,①
=1,①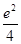 (
( )2-(
)2-(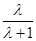 )2
)2 =1.②
=1.② =-1,③
=-1,③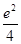 (4-4λ)=1+2λ,
(4-4λ)=1+2λ,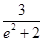
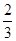 ≤λ≤
≤λ≤ 得,
得,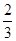 ≤1-
≤1-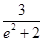 ≤
≤ ,
, ≤e≤
≤e≤ ,
, ,
, ].
].

科目:高中数学 来源:不详 题型:解答题
 (
( 为正常数),点
为正常数),点 在
在 轴的负半轴上,点
轴的负半轴上,点 在
在 轴上,且
轴上,且 ,
, .
.  在
在
 轴上运动时,求点
轴上运动时,求点 的轨迹
的轨迹 的方程;
的方程; 过点
过点 且与曲线
且与曲线 相交于不同两点
相交于不同两点 ,分别过点
,分别过点 作直线
作直线 :
: 的
的 垂线,对应的垂足分别为
垂线,对应的垂足分别为
 ,求
,求 的值;
的值; ,
, ,
, ,
, ,求
,求 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
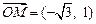 ,向量
,向量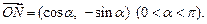
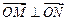 ,求
,求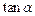 的值;
的值;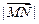 的最大值及此时
的最大值及此时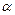 的值。
的值。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 =(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为|
=(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为| |个单位.设开始
|个单位.设开始 时点P的坐标为(-10,10),则5秒后点P的坐标为
时点P的坐标为(-10,10),则5秒后点P的坐标为  ( )
( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com