
 ,且
,且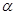 、
、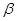 均为锐角,求
均为锐角,求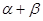 的值。
的值。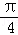
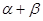 的正弦,这时由于正弦函数在
的正弦,这时由于正弦函数在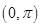 区间内不单调故满足条件的角有两个,两个是否都满足还需进一步检验这就给解答带来了困难,但若求
区间内不单调故满足条件的角有两个,两个是否都满足还需进一步检验这就给解答带来了困难,但若求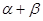 的余弦就不易出错,这是因为余弦函数在
的余弦就不易出错,这是因为余弦函数在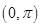 内单调,满足条件的角唯一。
内单调,满足条件的角唯一。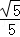 ,sinβ=
,sinβ=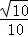 ,
,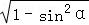 =
=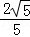
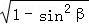 =
=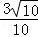
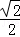
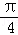
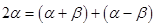 等。二是依据三角函数值求角时要注意确定角的范围的技巧。
等。二是依据三角函数值求角时要注意确定角的范围的技巧。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com