
分析 (1)根据正弦定理将原式转化成sinAcosC+$\frac{1}{2}$sinC=sinB,利用三角形的内角和为π及两角和的正弦求得cosA的值,根据A的取值范围,即可求得A的大小;
(2)由正弦定理及(1)可知:b=sinB,c=sinC,将b+c转化成$\sqrt{3}$sin(B+$\frac{π}{6}$),根据正弦函数图象及性质及B的取值范围,即可求得b+c的取值范围.
解答 解:(1)∵cosC+$\frac{1}{2}$c=b.
根据正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$,
∴sinAcosC+$\frac{1}{2}$sinC=sinB,
在三角形中:A+B+C=π,
sinB=sin(A+C)=sinAcosC+cosAsinC,
∴sinAcosC+$\frac{1}{2}$sinC=sinAcosC+cosAsinC,
$\frac{1}{2}$sinC=cosAsinC,
∵sinC≠0,
∴cosA=$\frac{1}{2}$,
∵0<A<π,
A=$\frac{π}{3}$;
(2)由正弦定理可知:$\frac{b}{sinB}=\frac{c}{sinC}=\frac{a}{sinA}$=$\frac{\frac{\sqrt{3}}{2}}{sin\frac{π}{3}}$=1,
∴b=sinB,c=sinC,
∴b+c=sinB+sinC=sinB+sin($\frac{2π}{3}$-B)=$\sqrt{3}$sin(B+$\frac{π}{6}$),
∵0<B<$\frac{2π}{3}$,
∴$\frac{π}{6}$<B+$\frac{π}{6}$<$\frac{5π}{6}$,
$\frac{1}{2}$<sin(B+$\frac{π}{6}$)≤1
∴$\frac{\sqrt{3}}{2}$<b+c≤$\sqrt{3}$,
∴b+c的取值范围.($\frac{\sqrt{3}}{2}$,$\sqrt{3}$].
点评 本题考查正弦定理及三角恒等变形相结合,考查正弦函数的性质,考查综合分析问题及解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题

| A. | $\frac{27\sqrt{3}}{2}$ | B. | $\frac{27\sqrt{35}}{2}$ | C. | $\frac{27}{2}$($\sqrt{3}$+$\sqrt{35}$) | D. | $\frac{27}{2}$($\sqrt{35}$-$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
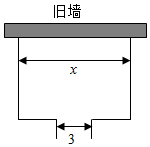 如图所示,要围建一个面积为400m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙时需要维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为3m的进出口,已知旧墙的维修费用为56元/m,新墙的造价为200元/m,设利用旧墙的长度为x(单位:m),修建此矩形场地的总费用为y(单位:元).
如图所示,要围建一个面积为400m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙时需要维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为3m的进出口,已知旧墙的维修费用为56元/m,新墙的造价为200元/m,设利用旧墙的长度为x(单位:m),修建此矩形场地的总费用为y(单位:元).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(K2≥K) | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.635 | 10.828 |
| A. | 有99%以上的把握认为“爱好该项运动与性别有关” | |
| B. | 有99%以上的把握认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com