
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=![]() AB.
AB.

(1)证明:BC1∥平面A1CD;
(2)求二面角D-A1C-E的余弦值.
科目:高中数学 来源: 题型:
【题目】我们知道,地球上的水资源有限,爱护地球、节约用水是我们每个人的义务与责任.某市政府为了对自来水的使用进行科学管理,节约水资源,计划确定一个家庭年用水量的标准.为此,对全市家庭日常用水量的情况进行抽样抽查,获得了![]() 个家庭某年的用水量(单位:立方米),统计结果如下表及图所示.
个家庭某年的用水量(单位:立方米),统计结果如下表及图所示.
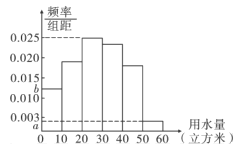
分组 | 频数 | 频率 |
| 25 | |
| 0.19 | |
| 50 | |
| 0.23 | |
| 0.18 | |
| 5 |
(1)分别求出![]() ,
,![]() 的值;
的值;
(2)若以各组区间中点值代表该组的取值,试估计全市家庭年均用水量;
(3)从样本中年用水量在![]() (单位:立方米)的5个家庭中任选3个,作进一步的跟踪研究,求年用水量最多的家庭被选中的概率(5个家庭的年用水量都不相等).
(单位:立方米)的5个家庭中任选3个,作进一步的跟踪研究,求年用水量最多的家庭被选中的概率(5个家庭的年用水量都不相等).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一组数据中的每一个数据都乘以2,再减去80,得到一组新数据,若求得新的数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
A.40.6,1.1B.48.8,4.4C.81.2,44.4D.78.8,75.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棱长为1的正方体![]() 中,点
中,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上运动(不包括线段端点),且
上运动(不包括线段端点),且![]() .以下结论:①
.以下结论:①![]() ;②若点
;②若点![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,则由线
的中点,则由线![]() 与
与![]() 确定的平面在正方体
确定的平面在正方体![]() 上的截面为等边三角形;③四面体
上的截面为等边三角形;③四面体![]() 的体积的最大值为
的体积的最大值为![]() ;④直线
;④直线![]() 与直线
与直线![]() 的夹角为定值.其中正确的结论为______.(填序号)
的夹角为定值.其中正确的结论为______.(填序号)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图2).
(如图2).![]() 为
为![]() 中点
中点
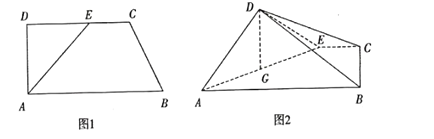
(1)求证:![]() ;
;
(2)求四棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,且
,且![]() ,则
,则
①数列![]() 是等比数列;
是等比数列;
②满足不等式:![]()
③若函数![]() 在R上单调递减,则数列
在R上单调递减,则数列![]() 是单调递减数列;
是单调递减数列;
④存在数列![]() 中的连续三项,能组成三角形的三条边;
中的连续三项,能组成三角形的三条边;
⑤满足等式:![]() .
.
正确的序号是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以![]() 为首项的数列
为首项的数列![]() 满足:
满足: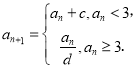
(1)当![]() ,
,![]() 时,求数列
时,求数列![]() 的通项公式;
的通项公式;
(2)当![]() ,
,![]() 时,试用
时,试用![]() 表示数列
表示数列![]() 前100项的和
前100项的和![]() ;
;
(3)当![]() (
(![]() 是正整数),
是正整数),![]() ,正整数
,正整数![]() 时,判断数列
时,判断数列![]() ,
,![]() ,
,![]() ,
,![]() 是否成等比数列?并说明理由.
是否成等比数列?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com