
分析 (1)根据题意,函数v(x)表达式为分段函数的形式,关键在于求函数v(x)在20≤x≤200时的表达式,根据一次函数表达式的形式,用待定系数法可求得;
(2)先在0≤x≤20上,车流量函数为增函数,得最大值为v(20)=1200,然后在20≤x≤200上,车流量函数为二次函数,然后根据二次函数的最大值问题解答.
解答 解:(1)由题意:当0≤x≤20时,v=60,
当20<x≤200时,设v=kx+b,
根据题意得,$\left\{\begin{array}{l}{200k+b=0}\\{20k+b=60}\end{array}\right.$,
解得k=-$\frac{1}{3}$,b=$\frac{200}{3}$,
所以,函数解析式为v=-$\frac{1}{3}$x+$\frac{200}{3}$,
故车流速度v关于x的解析式为v=$\left\{\begin{array}{l}{60,0≤x≤20}\\{-\frac{1}{3}x+\frac{200}{3},20<x≤200}\end{array}\right.$;
(2)依题并由(1)可得车流量v(x)=60x(0≤x<20),
v(x)=x(-$\frac{1}{3}$x+$\frac{200}{3}$)=-$\frac{1}{3}$(x-100)2+$\frac{10000}{3}$,(20≤x≤200),
当0≤x<20时,v(x)为增函数,故当x=20时,其最大值为60×20=1200,
当20≤x≤200时,当x=100时,v(x)最大,最大值为=$\frac{10000}{3}$≈3333,
综上所述,当x=100时,最大值约为3333.
答:(1)函数v关于x的解析式为v=$\left\{\begin{array}{l}{60,0≤x≤20}\\{-\frac{1}{3}x+\frac{200}{3},20<x≤200}\end{array}\right.$;
(2)x=100时,最大值约为3333.
点评 本题主要考查一次函数的应用、最值等基础知识,同时考查运用数学知识解决实际问题的能力,属于中等题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{4}{5}$ | C. | log23 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
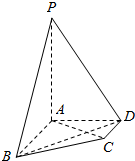 在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.
在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
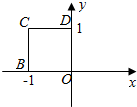 已知函数f(x)=$|\begin{array}{l}{x}\end{array}|,x∈[a,b]$值域是[0,1],那么点p(a,b) 在平面角坐标系中的位置位于图中的( )
已知函数f(x)=$|\begin{array}{l}{x}\end{array}|,x∈[a,b]$值域是[0,1],那么点p(a,b) 在平面角坐标系中的位置位于图中的( )| A. | 线段OB和OD | B. | 线段BC和CD | C. | 线段BC和BO | D. | 线段OB和CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com