
【题目】已知函数![]() =ex(ex﹣a)﹣a2x.
=ex(ex﹣a)﹣a2x.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)见解析(2)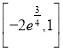
【解析】试题分析:(1)先求函数导数![]() ,再按导函数零点讨论:若
,再按导函数零点讨论:若![]() ,无零点,单调;若
,无零点,单调;若![]() ,一个零点
,一个零点![]() ,先减后增;若
,先减后增;若![]() ,一个零点
,一个零点![]() ,先减后增;(2)由单调性确定函数最小值:若
,先减后增;(2)由单调性确定函数最小值:若![]() ,满足;若
,满足;若![]() ,最小值为
,最小值为![]() ,即
,即![]() ;若
;若![]() ,最小值为
,最小值为![]() ,即
,即![]() ,综合可得
,综合可得![]() 的取值范围为
的取值范围为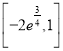 .
.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
①若![]() ,则
,则![]() ,在
,在![]() 单调递增.
单调递增.
②若![]() ,则由
,则由![]() 得
得![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
③若![]() ,则由
,则由![]() 得
得![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)①若![]() ,则
,则![]() ,所以
,所以![]() .
.
②若![]() ,则由(1)得,当
,则由(1)得,当![]() 时,
时, ![]() 取得最小值,最小值为
取得最小值,最小值为![]() .从而当且仅当
.从而当且仅当![]() ,即
,即![]() 时,
时, ![]() .
.
③若![]() ,则由(1)得,当
,则由(1)得,当![]() 时,
时, ![]() 取得最小值,最小值为
取得最小值,最小值为![]() .从而当且仅当
.从而当且仅当![]() ,即
,即![]() 时
时![]() .
.
综上, ![]() 的取值范围为
的取值范围为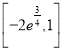 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设函数fn(x)=xn+bx+c(n∈N* , b,c∈R)
(Ⅰ)设n≥2,b=1,c=﹣1,证明:fn(x)在区间( ![]() )内存在唯一的零点;
)内存在唯一的零点;
(Ⅱ)设n=2,若对任意x1 , x2∈[﹣1,1],均有|f2(x1)﹣f2(x2)丨≤4,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C: ![]() 经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
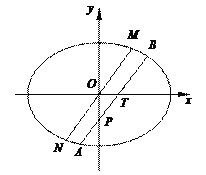
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求 ![]() 的值;
的值;
(3)记直线l与y轴的交点为P.若![]() ,求直线l的斜率k.
,求直线l的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个(其中“贝贝”、“晶晶”、“欢欢”、“迎迎”和“妮妮各一个”),现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲赢得乙一个福娃;否则乙赢得甲一个福娃,规定掷骰子的次数达9次时,或在此前某人已赢得所有福娃时游戏终止.记游戏终止时投掷骰子的次数为ξ
(1)求掷骰子的次数为7的概率;
(2)求ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=k﹣2i(k∈R)的共轭复数 ![]() ,且z﹣(
,且z﹣( ![]() ﹣i)=
﹣i)= ![]() ﹣2i.
﹣2i.
(1)求k的值;
(2)若过点(0,﹣2)的直线l的斜率为k,求直线l与曲线y= ![]() 以及y轴所围成的图形的面积.
以及y轴所围成的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com