
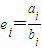 且ai<bi,由所有ei组成的集合设为:A={e1,e2,…,ek},则k的值为 ;设集合B=
且ai<bi,由所有ei组成的集合设为:A={e1,e2,…,ek},则k的值为 ;设集合B=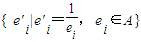 ,对任意ei∈A,e'j∈B,则ei+e'j∈M的概率为
,对任意ei∈A,e'j∈B,则ei+e'j∈M的概率为 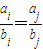 的二元子集有:
的二元子集有: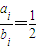 ,
,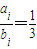 ,{2,3},{4,6},这时
,{2,3},{4,6},这时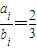 ,
,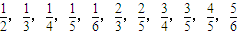 }
}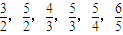 }
}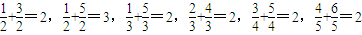 共6对.
共6对.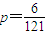 .
.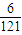 .
.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com