
【题目】如图,在正三棱柱ABC﹣A1B1C1中,已知D,E分别为BC,B1C1的中点,点F在棱CC1上,且EF⊥C1D.求证: 
(1)直线A1E∥平面ADC1;
(2)直线EF⊥平面ADC1 .
【答案】
(1)证明:连接ED,∵D,E分别为BC,B1C1的中点,
∴B1E∥BD且B1E=BD,
∴四边形B1BDE是平行四边形,
∴BB1∥DE且BB1=DE,又BB1∥AA1且BB1=AA1,
∴AA1∥DE且AA1=DE,
∴四边形AA1ED是平行四边形,
∴A1E∥AD,又∵A1E平面ADC1,AD平面ADC1,
∴直线A1E∥平面ADC1
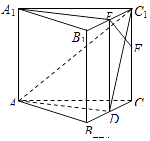
(2)证明:在正三棱柱ABC﹣A1B1C1中,BB1⊥平面ABC,
又AD平面ABC,所以AD⊥BB1,
又△ABC是正三角形,且D为BC的中点,∴AD⊥BC,
又BB1,BC平面B1BCC1,BB1∩BC=B,
∴AD⊥平面B1BCC1,
又EF平面B1BCC1,∴AD⊥EF,
又EF⊥C1D,C1D,AD平面ADC1,C1D∩AD=D,
∴直线EF⊥平面ADC1
【解析】(1)连接ED,∵D,E分别为BC,B1C1的中点.可得四边形B1BDE是平行四边形,进而证明四边形AA1ED是平行四边形,再利用线面平行的判定定理即可证明直线A1E∥平面ADC1 . (2)在正三棱柱ABC﹣A1B1C1中,利用线面垂直的判定与性质定理可得AD⊥BB1 , 又△ABC是正三角形,可得AD⊥BC,再利用线面垂直的判定定理即可证明结论.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
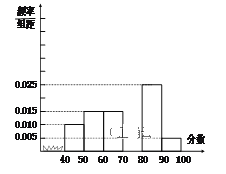
【题目】某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
(1)求第四小组的频率![]() ;
;
(2)估计这次考试的平均分和中位数(精确到0.01);
(3)从成绩是40~50分及90~100分的学生中选两人,记他们的成绩分别为![]() ,求满足“
,求满足“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地建一座桥,两端的桥墩已建好,这两墩相距640米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为![]() 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为![]() 万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,设需要新建
万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,设需要新建![]() 个桥墩,记余下工程的费用为
个桥墩,记余下工程的费用为![]() 万元.
万元.
(1)试写出![]() 关于
关于![]() 的函数关系式;(注意:
的函数关系式;(注意:![]() )
)
(2)需新建多少个桥墩才能使![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的职工食堂中,食堂每天以![]() 元/个的价格从面包店购进面包,然后以
元/个的价格从面包店购进面包,然后以![]() 元/个的价格出售.如果当天卖不完,剩下的面包以
元/个的价格出售.如果当天卖不完,剩下的面包以![]() 元/个的价格全部卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了
元/个的价格全部卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了![]() 个面包,以
个面包,以![]() (单位:个,
(单位:个,![]() )表示面包的需求量,
)表示面包的需求量,![]() (单位:元)表示利润.
(单位:元)表示利润.

(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)根据直方图估计利润![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ax2+ax,a为正实数.
(1)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求证:f( ![]() )≤0;
)≤0;
(3)若函数f(x)有且只有1个零点,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,是假命题的是( )
A.?x0∈R,sinx0+cosx0= ![]()
B.?x0∈R,tanx0=2016
C.?x>0,x>lnx
D.?x∈R,2x>0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足(p﹣1)Sn=p2﹣an(p>0,p≠1),且a3= ![]() .
.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bnbn+2}的前n项和为Tn , 若对于任意的正整数n,都有Tn<m2﹣m+
,数列{bnbn+2}的前n项和为Tn , 若对于任意的正整数n,都有Tn<m2﹣m+ ![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线C: ![]() =1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=
=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ= ![]() ,且
,且 ![]() |,则双曲线C的离心率为( )
|,则双曲线C的离心率为( ) 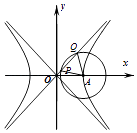
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com