练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，圆，点，为抛物线上任意一点（异于原点），过点作圆的切线，为切点，则的最小值是___．

    【答案】3

    【解析】

    设P（x，y），可得y2＝2x，求得圆M的圆心和半径，求得切线长|PB|，化简可得|PB|为P到y轴的距离，结合抛物线的定义和三点共线取得最值的性质，即可得到所求最小值．

    解：设P（x，y），可得y2＝2x，

    圆M：（x﹣1）2+y2＝1的圆心M（1，0），半径为1，

    |PB||x|，

    即|PB|为P到y轴的距离，

    抛物线的焦点F（，0），准线方程为x，

    可得|PA|+|PB|＝|PA|+|PK||PA|+|PF|，

    过A作准线的垂线，垂足为K，可得A，P，K共线时，|PA|+|PK|取得最小值|AK|，

    即有|PA|+|PB|的最小值为3．

    故答案为：3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数f(x)的定义域为D＝{x|x≠0}，且满足对于任意x1，x2∈D，有f(x1·x2)＝f(x1)＋f(x2)．

    (1)求f(1)的值；

    (2)判断f(x)的奇偶性并证明你的结论；

    (3)如果f(4)＝1，f(x－1)<2，且f(x)在(0，＋∞)上是增函数，求x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，圆，点，为抛物线上任意一点（异于原点），过点作圆的切线，为切点，则的最小值是___．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“双十二”是继“双十一”之后的又一个网购狂欢节，为了刺激“双十二”的消费，某电子商务公司决定对“双十一”的网购者发放电子优惠券.为此，公司从“双十一”的网购消费者中用随机抽样的方法抽取了100人，将其购物金额（单位：万元）按照， 分组，得到如下频率分布直方图：

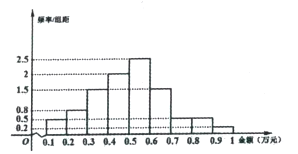
    根据调查，该电子商务公司制定了发放电子优惠券的办法如下：

    （1）求购物者获得电子优惠券金额的平均数；

    （2）从购物者中随机抽取10人，这10人中获得电子优惠券的人数为，求的数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，点，分别是椭圆 的左、右焦点，过点且与轴垂直的直线与椭圆交于，两点．若为锐角，则该椭圆的离心率的取值范围是_____

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于定义域为D的函数，若存在区间，使得同时满足，①在上是单调函数，②当的定义域为时，的值域也为，则称区间为该函数的一个“和谐区间”

    （1）求出函数的所有“和谐区间”；

    （2）函数是否存在“和谐区间”？若存在，求出实数a，b的值；若不存在，请说明理由

    （3）已知定义在上的函数有“和谐区间”，求正整数k取最小值时实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次社会实践活动中，某数学调研小组根据车间持续5个小时的生产情况画出了某种产品的总产量（单位：千克）与时间（单位：小时）的函数图像，则以下关于该产品生产状况的正确判断是（ ）.

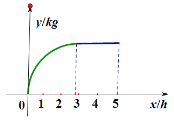
    A.在前三小时内，每小时的产量逐步增加

    B.在前三小时内，每小时的产量逐步减少

    C.最后一小时内的产量与第三小时内的产量相同

    D.最后两小时内，该车间没有生产该产品

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xoy中，曲线C1的参数方程为以原点O为极点，x轴正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为

    （1）求曲线C1与C2的直角坐标方程；

    （2）当C1与C2有两个公共点时，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商品在近30天内每件的销售价格p(元)与时间t(天)的函数关系是该商品的日销售量Q(件)与时间t(天)的函数关系是Q＝－t＋40(0<t≤30，t∈N)．

    (1)求这种商品的日销售金额的解析式；

    (2)求日销售金额的最大值，并指出日销售金额最大的一天是30天中的第几天？

    查看答案和解析>>

    同步练习册答案