
ĄūĖâÄŋĄŋÄģģ§ļųūÝĘÐģĄÐčĮóŋŠ·ĒČý―ĮŧĻĀšÖ§žÜĢĻČįÍžĢĐĢŽÉÏÃæΊŧĻĀšĢŽÖ§žÜÓÉČýļųÏļļÖđÜŨéģÉĢŽŋžÂĮĩ―ļÖđÜĩÄĘÜÁĶšÍŧĻĀšÖĘÁŋĩČŌōËØĢŽÉčžÆÖ§žÜÓĶÂúŨãĢšĒŲČýļųÏļļÖđÜģĪūųΊ1ÃŨĢĻīÖÏļšöÂÔēŧžÆĢĐĢŽĮŌÓëĩØÃæËųģÉĩÄ―ĮūųΊ![]() ĢŧĒÚžÜÃæÓëžÜĩŨÆ―ÐÐĢŽĮŌžÜÃæČý―ĮÐÎ
ĢŧĒÚžÜÃæÓëžÜĩŨÆ―ÐÐĢŽĮŌžÜÃæČý―ĮÐÎ![]() ÓëžÜĩŨČý―ĮÐÎ
ÓëžÜĩŨČý―ĮÐÎ![]() ūųΊĩČąßČý―ĮÐÎĢŧĒÛČýļųÏļļÖđÜÏā―ŧīĶĩÄ―Úĩã
ūųΊĩČąßČý―ĮÐÎĢŧĒÛČýļųÏļļÖđÜÏā―ŧīĶĩÄ―Úĩã![]() ·ÖČýļųÏļļÖđÜÉÏĄĒÏÂÁ―ķÎÖŪąČūųΊ
·ÖČýļųÏļļÖđÜÉÏĄĒÏÂÁ―ķÎÖŪąČūųΊ![]() .ķĻŌåĢšžÜÃæÓëžÜĩŨĩÄūāĀëΊĄ°Ö§žÜļßķČĄąĢŽžÜĩŨČý―ĮÐÎ
.ķĻŌåĢšžÜÃæÓëžÜĩŨĩÄūāĀëΊĄ°Ö§žÜļßķČĄąĢŽžÜĩŨČý―ĮÐÎ![]() ĩÄÃæŧýÓ륰֧žÜļßķČĄąĩÄģËŧýΊĄ°Ö§žÜÐčŌŠŋÕžäĄą.
ĩÄÃæŧýÓ륰֧žÜļßķČĄąĩÄģËŧýΊĄ°Ö§žÜÐčŌŠŋÕžäĄą.
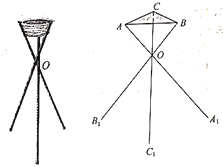
ĢĻ1ĢĐĩą![]() ĘąĢŽĮóĄ°Ö§žÜļßķČĄąĢŧ
ĘąĢŽĮóĄ°Ö§žÜļßķČĄąĢŧ
ĢĻ2ĢĐĮóĄ°Ö§žÜÐčŌŠŋÕžäĄąĩÄŨîīóÖĩ.
Ąūīð°ļĄŋĢĻ1ĢĐ![]() ÃŨ.ĢĻ2ĢĐ
ÃŨ.ĢĻ2ĢĐ![]() ÁĒ·―ÃŨ.
ÁĒ·―ÃŨ.
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝĖâŌâ![]() ÓëĩØÃæËųģÉĩÄ―ĮΊ
ÓëĩØÃæËųģÉĩÄ―ĮΊ![]() ĢŽ
ĢŽ![]() ÃŨĢŽīÓķø
ÃŨĢŽīÓķø![]() .
.
ĢĻ2ĢĐđý![]() Ũũ
Ũũ![]() Æ―Ãæ
Æ―Ãæ![]() ĢŽīđŨãΊ
ĢŽīđŨãΊ![]() ĢŽĮŌ
ĢŽĮŌ![]() ĢŽąíĘūģö
ĢŽąíĘūģö![]() ĢŽ―øķø
ĢŽ―øķø![]() ĢŽ
ĢŽ![]() ĢŽÁî
ĢŽÁî![]() ĢŽĀûÓÃĩžĘýžīŋÉĮó―â.
ĢŽĀûÓÃĩžĘýžīŋÉĮó―â.
―âĢšĢĻ1ĢĐŌōΊžÜÃæÓëžÜĩŨÆ―ÐÐĢŽĮŌ![]() ÓëĩØÃæËųģÉĩÄ―ĮΊ
ÓëĩØÃæËųģÉĩÄ―ĮΊ![]() ĢŽ
ĢŽ![]() ÃŨĢŽ
ÃŨĢŽ
ËųŌÔĄ°Ö§žÜļßķČĄą![]() ĢĻÃŨĢĐ.
ĢĻÃŨĢĐ.
ĢĻ2ĢĐđý![]() Ũũ
Ũũ![]() Æ―Ãæ
Æ―Ãæ![]() ĢŽīđŨãΊ
ĢŽīđŨãΊ![]() .
.
ÓÖ![]() Æ―Ãæ
Æ―Ãæ![]() ĢŽËųŌÔ
ĢŽËųŌÔ![]() ĢŽ
ĢŽ
ÓÖ![]() ÓëĩØÃæËųģÉĩÄ―ĮΊ
ÓëĩØÃæËųģÉĩÄ―ĮΊ![]() ĢŽËųŌÔ
ĢŽËųŌÔ![]() ĢŽ
ĢŽ
ÍŽĀí![]() ĢŽ
ĢŽ
ËųŌÔ![]() ΊĩČąßČý―ĮÐÎ
ΊĩČąßČý―ĮÐÎ![]() ÍâÐÄĢŽŌēΊÆäÖØÐÄĢŽ
ÍâÐÄĢŽŌēΊÆäÖØÐÄĢŽ
ËųŌÔ![]() ĢŽ
ĢŽ
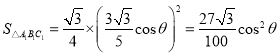 ĢŽ
ĢŽ
žĮĄ°Ö§žÜÐčŌŠŋÕžäĄąÎŠ![]() ĢŽÔō
ĢŽÔō![]() ĢŽ
ĢŽ![]() .
.
Áî![]() ĢŽÔō
ĢŽÔō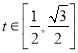 .
.
ËųŌÔ![]() ĢŽ
ĢŽ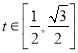 .
.
ÓÖ![]()
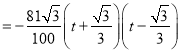 ĢŽ
ĢŽ
Ôōĩą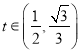 ĘąĢŽ
ĘąĢŽ![]() ĢŽ
ĢŽ![]() ĩĨĩũĩÝÔöĢŧĩą
ĩĨĩũĩÝÔöĢŧĩą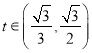 ĘąĢŽ
ĘąĢŽ![]() ĢŽ
ĢŽ![]() ĩĨĩũĩÝžõ.
ĩĨĩũĩÝžõ.
ËųŌÔĩą![]() ĘąĢŽ
ĘąĢŽ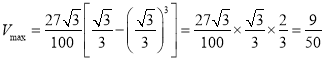 ĢĻÁĒ·―ÃŨĢĐ.
ĢĻÁĒ·―ÃŨĢĐ.
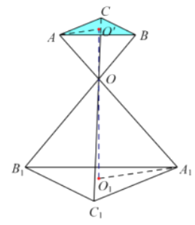
īðĢšĢĻ1ĢĐĩą![]() ĘąĢŽĄ°Ö§žÜļßķČĄąÎŠ
ĘąĢŽĄ°Ö§žÜļßķČĄąÎŠ![]() ÃŨĢŧ
ÃŨĢŧ
ĢĻ2ĢĐĄ°Ö§žÜÐčŌŠŋÕžäĄąĩÄŨîīóÖĩΊ![]() ÁĒ·―ÃŨ.
ÁĒ·―ÃŨ.



| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋËÄĀâŨķS-ABCDÖÐĢŽĩŨÃæABCDĘĮąßģĪΊ2ĩÄÁâÐÎĢŽ![]() ĢŽ
ĢŽ![]() ĢŽķþÃæ―ĮS-BD-CĩÄÓāÏŌÖĩΊ
ĢŽķþÃæ―ĮS-BD-CĩÄÓāÏŌÖĩΊ![]() ĢŪ
ĢŪ
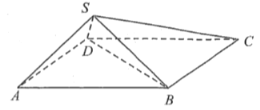
ĢĻIĢĐÖĪÃũĢšÆ―Ãæ![]() Æ―ÃæSBDĢŧ
Æ―ÃæSBDĢŧ
ĢĻĒōĢĐĮóķþÃæ―ĮA-SD-CĩÄÓāÏŌÖĩĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚËÄĀâŨķSĐABCDÖÐĢŽēāÃæSCDΊķÛ―ĮČý―ĮÐÎĮŌīđÖąÓÚĩŨÃæABCDĢŽCDĢ―SDĢŽĩãMĘĮSAĩÄÖÐĩãĢŽAD//BCĢŽĄÏABCĢ―90ĄãĢŽABĢ―AD![]() BCĢ―aĢŪ
BCĢ―aĢŪ

ĢĻ1ĢĐĮóÖĪĢšÆ―ÃæMBDĄÍÆ―ÃæSCDĢŧ
ĢĻ2ĢĐČôĄÏSDCĢ―120ĄãĢŽĮóČýĀâŨķCĐMBDĩÄĖåŧýĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠÖąÏß![]() Ģš
Ģš![]() ĢŽ°ëūķΊ2ĩÄÔē
ĢŽ°ëūķΊ2ĩÄÔē![]() Óë
Óë![]() ÏāĮÐĢŽÔēÐÄ
ÏāĮÐĢŽÔēÐÄ![]() ÔÚ
ÔÚ![]() ÖáÉÏĮŌÔÚÖąÏß
ÖáÉÏĮŌÔÚÖąÏß![]() ĩÄÓŌÉÏ·―.
ĩÄÓŌÉÏ·―.
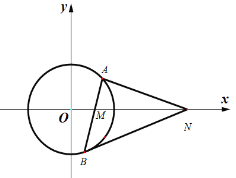
ĢĻ1ĢĐĮóÔē![]() ĩÄ·―ģĖĢŧ
ĩÄ·―ģĖĢŧ
ĢĻ2ĢĐđýĩã![]() ĩÄÖąÏßÓëÔē
ĩÄÖąÏßÓëÔē![]() ―ŧÓÚ
―ŧÓÚ![]() ĢŽ
ĢŽ![]() Á―ĩãĢĻ
Á―ĩãĢĻ![]() ÔÚ
ÔÚ![]() ÖáÉÏ·―ĢĐĢŽÎĘÔÚ
ÖáÉÏ·―ĢĐĢŽÎĘÔÚ![]() ÖáÕý°ëÖáÉÏĘĮ·ņīæÔÚķĻĩã
ÖáÕý°ëÖáÉÏĘĮ·ņīæÔÚķĻĩã![]() ĢŽĘđĩÃ
ĢŽĘđĩÃ![]() ÖáÆ―·Ö
ÖáÆ―·Ö![]() ĢŋČôīæÔÚĢŽĮëĮóģöĩã
ĢŋČôīæÔÚĢŽĮëĮóģöĩã![]() ĩÄŨøąęĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉ.
ĩÄŨøąęĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÔÚËÄĀâŨķP-ABCDĢŽËÄąßÐÎABCDĘĮąßģĪΊ3ĩÄÕý·―ÐÎĢŽÆ―Ãæ![]() Æ―Ãæ
Æ―Ãæ![]() ĢŽ
ĢŽ![]() ÓÚĩãOĢŽ
ÓÚĩãOĢŽ![]() ĢŽĩãEÔÚĀâPBÉÏĢŽ
ĢŽĩãEÔÚĀâPBÉÏĢŽ![]() .
.
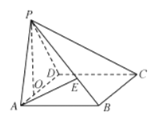
ĢĻ1ĢĐĩą![]() ĘąĢŽĮóÖąÏßAEÓëÆ―ÃæPCDËųģÉ―ĮĩÄÕýÏŌÖĩĢŧ
ĘąĢŽĮóÖąÏßAEÓëÆ―ÃæPCDËųģÉ―ĮĩÄÕýÏŌÖĩĢŧ
ĢĻ2ĢĐČôķþÃæ―ĮB-PC-DĩÄÓāÏŌÖĩΊ![]() ĢŽĮóPOĩÄģĪ.
ĢŽĮóPOĩÄģĪ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįđûķÔÄģķÔÏóÁŽÐøĘĩĘĐÁ―īÎąäŧŧšóĩÄ―áđûūÍĘĮąäŧŧĮ°ĩÄķÔÏóĢŽÄĮÃīÎŌÃĮģÆÕâÖÖąäŧŧΊĄ°ŧØđ饹ąäŧŧ.ČįĢšķÔČÎŌâŌŧļöĘĩĘýĢŽąäŧŧĢšČĄÆäÏā·īĘý.ŌōΊÏā·īĘýĩÄÏā·īĘýĘĮËüąūÉíĢŽËųŌÔąäŧŧĄ°ČĄĘĩĘýĩÄÏā·īĘýĄąĘĮŌŧÖÖĄ°ŧØđ饹ąäŧŧ.ÓÐÏÂÁÐ3ÖÖąäŧŧĢš
ĒŲķÔ![]() ĢŽąäŧŧĢšĮóžŊšÏAĩÄēđžŊĢŧ
ĢŽąäŧŧĢšĮóžŊšÏAĩÄēđžŊĢŧ
ĒÚķÔČÎŌâ![]() ĢŽąäŧŧĢšĮózĩÄđēéîļīĘýĢŧ
ĢŽąäŧŧĢšĮózĩÄđēéîļīĘýĢŧ
ĒÛķÔČÎŌâ![]() ĢŽąäŧŧĢš
ĢŽąäŧŧĢš![]() ĢĻkĢŽbūųΊ·ĮÁãĘĩĘýĢĐ.
ĢĻkĢŽbūųΊ·ĮÁãĘĩĘýĢĐ.
ÆäÖÐĘĮĄ°ŧØđ饹ąäŧŧĩÄĘĮ______.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋĄķŌŨūĄ·ĘĮÖÐđúīŦÍģÎÄŧŊÖÐĩÄūŦËčĢŽČįÍžĘĮŌŨū°ËØÔĢĻšŽĮŽĄĒĀĪĄĒŲãĄĒÕðĄĒŋēĄĒĀëĄĒôÞĄĒķŌ°ËØÔĢĐĢŽÃŋŌŧØÔÓÉČýļųÏßŨéģÉĢĻ"![]() "ąíĘūŌŧļųŅôÏßĢŽ"
"ąíĘūŌŧļųŅôÏßĢŽ"![]() "ąíĘūŌŧļųŌõÏßĢĐĢŽīÓ°ËØÔÖÐČÎČĄÁ―ØÔĢŽÕâÁ―ØÔĩÄÁųļųÏßÖÐĮĄÓÐÁ―ļųŅôÏßĢŽËÄļųŌõÏßĩÄļÅÂĘΊ_______.
"ąíĘūŌŧļųŌõÏßĢĐĢŽīÓ°ËØÔÖÐČÎČĄÁ―ØÔĢŽÕâÁ―ØÔĩÄÁųļųÏßÖÐĮĄÓÐÁ―ļųŅôÏßĢŽËÄļųŌõÏßĩÄļÅÂĘΊ_______.

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚËÄĀâŨķ![]() ÖÐĢŽŌŅÖŠËÄąßÐÎ
ÖÐĢŽŌŅÖŠËÄąßÐÎ![]() ĘĮąßģĪΊ
ĘĮąßģĪΊ![]() ĩÄÕý·―ÐÎĢŽĩã
ĩÄÕý·―ÐÎĢŽĩã![]() ÔÚĩŨÃæ
ÔÚĩŨÃæ![]() ÉÏĩÄÉäӰΊĩŨÃæ
ÉÏĩÄÉäӰΊĩŨÃæ![]() ĩÄÖÐÐÄĩã
ĩÄÖÐÐÄĩã![]() ĢŽĩã
ĢŽĩã![]() ÔÚĀâ
ÔÚĀâ![]() ÉÏĢŽĮŌ
ÉÏĢŽĮŌ![]() ĩÄÃæŧýΊ1ĢŪ
ĩÄÃæŧýΊ1ĢŪ
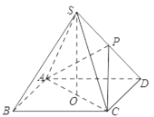
ĢĻ1ĢĐČôĩã![]() ĘĮ
ĘĮ![]() ĩÄÖÐĩãĢŽĮóÖĪĢšÆ―Ãæ
ĩÄÖÐĩãĢŽĮóÖĪĢšÆ―Ãæ![]() Æ―Ãæ
Æ―Ãæ![]() Ģŧ
Ģŧ
ĢĻ2ĢĐÔÚĀâ![]() ÉÏĘĮ·ņīæÔÚŌŧĩã
ÉÏĘĮ·ņīæÔÚŌŧĩã![]() ĘđĩÃķþÃæ―Į
ĘđĩÃķþÃæ―Į![]() ĩÄÓāÏŌÖĩΊ
ĩÄÓāÏŌÖĩΊ![]() ĢŋČôīæÔÚĢŽĮóģöĩã
ĢŋČôīæÔÚĢŽĮóģöĩã![]() ĩÄÎŧÖÃĢŧČôēŧīæÔÚĢŽËĩÃũĀíÓÉĢŪ
ĩÄÎŧÖÃĢŧČôēŧīæÔÚĢŽËĩÃũĀíÓÉĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
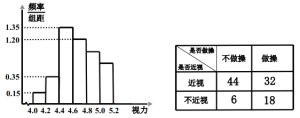
ĄūĖâÄŋĄŋŅÛąĢ―ĄēŲĘĮŌŧÖÖŅÛūĶĩÄąĢ―ĄĖåēŲĢŽÖũŌŠĘĮÍĻđý°īÄĶŅÛēŋŅĻÎŧĢŽĩũÕûŅÛž°Í·ēŋĩÄŅŠŌšŅŧ·ĢŽĩũ―ÚžĄČâĢŽļÄÉÆŅÛĩÄÆĢĀÍĢŽīïĩ―ÔĪ·Ā―üĘÓĩČŅÛēŋžēēĄĩÄÄŋĩÄ.ÄģŅ§ÐĢΊÁËĩũēéÍÆđãŅÛąĢ―ĄēŲķÔļÄÉÆŅ§ÉúĘÓÁĶĩÄЧđûĢŽÔÚÓĶ―ėļßČýĩÄČŦĖå800ÃûŅ§ÉúÖÐËæŧúģéČĄÁË100ÃûŅ§Éú―øÐÐĘÓÁĶžėēéĢŽēĒĩÃĩ―ČįÍžĩÄÆĩÂĘ·ÖēžÖą·―Íž.
ĢĻ1ĢĐČôÖą·―ÍžÖКóČýŨéĩÄÆĩĘýģÉĩČēîĘýÁÐĢŽĘÔđĀžÆČŦÄęžķĘÓÁĶÔÚ5.0ŌÔÉÏĩÄČËĘýĢŧ
ĢĻ2ĢĐΊÁËŅÐūŋŅ§ÉúĩÄĘÓÁĶÓëŅÛąĢ―ĄēŲĘĮ·ņÓÐđØÏĩĢŽķÔÄęžķēŧŨöŅÛąĢ―ĄēŲšÍžáģÖŨöŅÛąĢ―ĄēŲĩÄŅ§Éú―øÐÐÁËĩũēéĢŽĩÃĩ―ÏÂąíÖÐĘýūÝĢŽļųūÝąíÖÐĩÄĘýūÝĢŽÄÜ·ņÔÚ·ļīíĩÄļÅÂĘēŧģŽđý0.005ĩÄĮ°ĖáÏÂČÏΊĘÓÁĶÓëŅÛąĢ―ĄēŲÓÐđØÏĩĢŋ
ĢĻ3ĢĐÔÚĢĻ2ĢĐÖÐĩũēéĩÄ100ÃûŅ§ÉúÖÐĢŽ°īÕÕ·ÖēãģéŅųÔÚēŧ―üĘÓĩÄŅ§ÉúÖÐģéČĄ8ČËĢŽ―øŌŧē―ĩũēéËûÃĮÁžšÃĩÄŧĪŅÛÏ°đßĢŽÔÚÕâ8ČËÖÐČÎČĄ2ČËĢŽžĮžáģÖŨöŅÛąĢ―ĄēŲĩÄŅ§ÉúČËĘýΊXĢŽĮóXĩÄ·ÖēžÁКÍĘýŅ§ÆÚÍû.
ļ―Ģš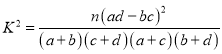
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com