
| 纪念币 | A | B | C | D |
| 概率 | 1/2 | 1/2 | a | a |
 ] ,2a+1
] ,2a+1 (1-
(1- )2
)2 (1-a)2=
(1-a)2= (1-a)2
(1-a)2
 (1-
(1- )
) (1-a)2+
(1-a)2+ (1-
(1- )2·
)2· a(1-a)=
a(1-a)=  (1-a)
(1-a)  (
( )2
)2 (1-a)2+
(1-a)2+
 (1-
(1- )
) a(1-a)+
a(1-a)+  (1-
(1- )2·
)2· a2=
a2= (1+2a-2 a2)
(1+2a-2 a2) (
( )2
)2 a(1-a)+
a(1-a)+ 
 (1-
(1- )
) a2=
a2=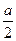
 (
( )2
)2 a2=
a2= a2 ……………………………………5分
a2 ……………………………………5分 (1+2a-2 a2)-
(1+2a-2 a2)-  =-
=- ≥0
≥0
 ,即a∈[
,即a∈[ ] ……………………9分
] ……………………9分 (1-a)2+1×
(1-a)2+1× (1-a)+2×
(1-a)+2× (1+2a-2a2)+3×
(1+2a-2a2)+3×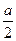 +4×
+4× =2a+1………………12分
=2a+1………………12分

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源:不详 题型:单选题
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 四个不同的赛场服务,每个赛场至少有一名志愿者。
四个不同的赛场服务,每个赛场至少有一名志愿者。 赛场服务的概率;
赛场服务的概率; 为这五名志愿者中参加
为这五名志愿者中参加 赛场服务的人数,求
赛场服务的人数,求 的分布列。
的分布列。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率 .
. ;
;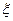 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求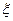 的分布列.
的分布列.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.至少有1个白球;都是白球. | B.至少有1个白球;至少有1个红球. |
| C.恰有1个白球;恰有2个白球. | D.至少有1个白球;都是红球 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.某辆汽车一年中发生事故的次数是一个离散型随机变量 |
| B.正态分布随机变量等于一个特定实数的概率为0 |
| C.公式EX=np可以用来计算离散型随机变量的均值 |
| D.从一副扑克牌中随机抽取5张,其中梅花的张数服从超几何分布 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.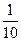 | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com