
如图,直线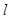 过点P(2,1),夹在两已知直线
过点P(2,1),夹在两已知直线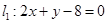 和
和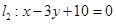 之间的线段AB恰被点P平分.
之间的线段AB恰被点P平分.
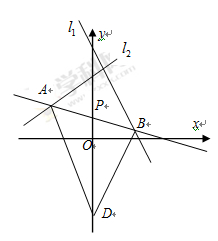
(1)求直线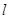 的方程;
的方程;
(2)设点D(0,m),且AD//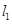 ,求:
,求: ABD的面积.
ABD的面积.
(1) 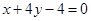 (2)
(2)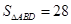
【解析】
试题分析:(1) 先点 在直线
在直线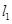 上设出
上设出 点的坐标,因为
点的坐标,因为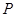 为线段
为线段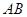 的中点,利用中点坐标公式即可列出两点坐标的两个关系式,得出
的中点,利用中点坐标公式即可列出两点坐标的两个关系式,得出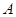 的坐标,把
的坐标,把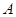 的坐标代入直线
的坐标代入直线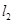 ,即可求出
,即可求出 的坐标,然后由
的坐标,然后由 和
和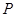 的坐标,利用两点式即可写出直线
的坐标,利用两点式即可写出直线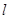 的方程.
的方程.
(2)由(1)知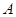 的坐标, 由AD//
的坐标, 由AD//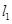 即
即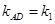 可得
可得 的坐标,由点到直线距离公式可求得点
的坐标,由点到直线距离公式可求得点 到
到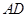 的距离,再由两点间距离公式求得
的距离,再由两点间距离公式求得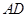 的长度.
的长度.
试题解析:
(1)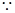 点B在直线
点B在直线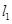 上,可设
上,可设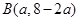 ,又P(0,1)是AB的中点,
,又P(0,1)是AB的中点, 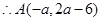
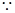 点A在直线
点A在直线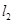 上,
上,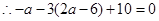
解得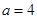 ,即
,即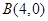 (4分)
(4分)
故直线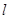 的方程是
的方程是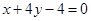 (6分)
(6分)
(2)由(1)知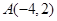 ,又
,又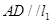 ,则
,则 (8分)
(8分)
点A到直线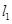 的距离
的距离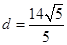 ,
,
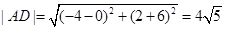 , (10分)
, (10分)
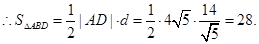 (12分)
(12分)
考点:两条直线的交点坐标;直线的一般式方程与直线的平行关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:

(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角α的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013年黑龙江省高三第四次联考理科数学试卷(解析版) 题型:解答题
已知抛物线E:y2=
4x,点P(2,O).如图所示,直线 .过点P且与抛物线E交于A(xl,y1)、B( x2,y2)两点,直线
.过点P且与抛物线E交于A(xl,y1)、B( x2,y2)两点,直线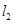 过点P且与抛物线E交于C(x3, y3)、D(x4,y4)两点.过点P作x轴的垂线,与线段AC和BD分别交于点M、N.
过点P且与抛物线E交于C(x3, y3)、D(x4,y4)两点.过点P作x轴的垂线,与线段AC和BD分别交于点M、N.

(I)求y1y2的值;
(Ⅱ)求讧:|PM|="|" PN|
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
如图所示,O为坐标原点,过点P(2,0)且斜率为k的直线L交抛物线y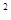 =2x于M(x
=2x于M(x ,y
,y ),N(x
),N(x ,y
,y )两点. ⑴写出直线L的方程;⑵求x
)两点. ⑴写出直线L的方程;⑵求x x
x 与y
与y y
y 的值;⑶求证:OM⊥ON
的值;⑶求证:OM⊥ON
查看答案和解析>>
科目:高中数学 来源:2013届度陕西省西安市高二第一学期期末理科数学试卷 题型:解答题
如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线
 于
于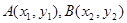 两点.
两点.
(1)
求 与
与 的值;(2)求证:
的值;(2)求证: .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com