Question

12．在边长为1的等边△ABC中，O为边AC的中点，BO为边AC上的中线，$\overrightarrow{BG}$=2$\overrightarrow{GO}$，设$\overrightarrow{CD}$∥$\overrightarrow{AG}$，若$\overrightarrow{AD}$=$\overrightarrow{AB}$+λ$\overrightarrow{AC}$（λ∈R），则|$\overrightarrow{AD}$|=$\sqrt{7}$．

Answer 1

分析 根据题意得出G是△ABC的重心，用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示出向量$\overrightarrow{AG}$，用$\overrightarrow{AG}$表示出$\overrightarrow{CD}$，写出$\overrightarrow{AD}$的表达式，利用向量相等列出方程组求出λ的值，代入$\overrightarrow{AD}$=$\overrightarrow{AB}$+λ$\overrightarrow{AC}$，计算得答案．

解答 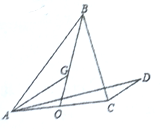解：由已知得G是三角形的重心，因此$\overrightarrow{AG}=\frac{1}{3}（\overrightarrow{AB}+\overrightarrow{AC}）$，
∵$\overrightarrow{CD}$∥$\overrightarrow{AG}$，设$\overrightarrow{CD}=k\overrightarrow{AG}$，
∴$\overrightarrow{CD}=\frac{k}{3}（\overrightarrow{AB}+\overrightarrow{AC}）$．
∴$\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{CD}$=$\frac{k}{3}\overrightarrow{AB}+（\frac{k}{3}+1）\overrightarrow{AC}$．
∵$\overrightarrow{AD}$=$\overrightarrow{AB}$+λ$\overrightarrow{AC}$，
∴$\left\{\begin{array}{l}{\frac{k}{3}=1}\\{λ=\frac{k}{3}+1}\end{array}\right.$，即λ=2．
∴$\overrightarrow{AD}$=$\overrightarrow{AB}$+2$\overrightarrow{AC}$，
∴${\overrightarrow{AD}}^{2}=（\overrightarrow{AB}+2\overrightarrow{AC}）^{2}$=$1+4+4×1×1×\frac{1}{2}=7$．
∴|$\overrightarrow{AD}$|=$\sqrt{7}$．
故答案为：$\sqrt{7}$．

点评 本题考查了向量在几何中的应用问题，也考查平面向量的基本定理，是中档题．