
【题目】在△ABC中,AB=AC,△ABC的外接圆⊙O的弦AD的延长线交BC的延长线于点E.
求证:△ABD∽△AEB.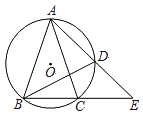
【答案】证明:∵AB=AC,∴∠ABC=∠ACB,
∵∠ACB与∠ADB所对应的弧为 ![]() .
.
∴∠ACB=∠ADB,
∴∠ADB=∠ABC,
又∠BAD共用,
∴△ABD∽△AEB
【解析】根据同弧所对的圆周角相等可知![]() ACB=
ACB=![]() ADB,从而得到
ADB,从而得到![]() ADB=
ADB=![]() ABC,然后根据“如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似”即可证明.
ABC,然后根据“如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似”即可证明.
【考点精析】关于本题考查的相似三角形的判定,需要了解相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,且f(1)=1,f(﹣2)=4.
,且f(1)=1,f(﹣2)=4.
(1)求a、b的值;
(2)已知定点A(1,0),设点P(x,y)是函数y=f(x)(x<﹣1)图象上的任意一点,求|AP|的最小值,并求此时点P的坐标;
(3)当x∈[1,2]时,不等式 ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的左顶点为A(﹣2,0),离心率为
=1(a>b>0)的左顶点为A(﹣2,0),离心率为 ![]() ,过点A的直线l与椭圆E交于另一点B,点C为y轴上的一点.
,过点A的直线l与椭圆E交于另一点B,点C为y轴上的一点.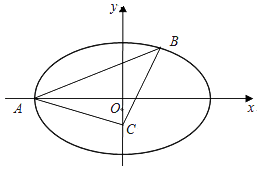
(1)求椭圆E的标准方程;
(2)若△ABC是以点C为直角顶点的等腰直角三角形,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(a2﹣3a+3)ax是指数函数,
(1)求f(x)的表达式;
(2)判断F(x)=f(x)﹣f(﹣x)的奇偶性,并加以证明
(3)解不等式:loga(1﹣x)>loga(x+2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b),
b), ![]() =(sinB,﹣cosA),且
=(sinB,﹣cosA),且 ![]() ⊥
⊥ ![]() .
.
(1)求A的大小;
(2)若| ![]() |=
|= ![]() ,求cosC的值.
,求cosC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为函数y=f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)图象的一部分,其中点 ![]() 是图象的一个最高点,点
是图象的一个最高点,点 ![]() 是与点P相邻的图象与x轴的一个交点.
是与点P相邻的图象与x轴的一个交点.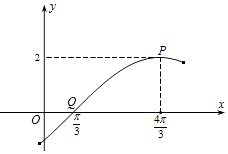
(1)求函数f(x)的解析式;
(2)若将函数f(x)的图象沿x轴向右平移 ![]() 个单位,再把所得图象上每一点的横坐标都变为原来的
个单位,再把所得图象上每一点的横坐标都变为原来的 ![]() (纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的单调递增区间.
(纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(Ⅰ)已知 ![]() ,其中ai∈R,i=1,2,…10.
,其中ai∈R,i=1,2,…10.
(i)求a0+a1+a2+…+a10;
(ii)求a7 .
(Ⅱ)2017年5月,北京召开“一带一路”国际合作高峰论坛.组委会将甲、乙、丙、丁、戊五名志愿者分配到翻译、导游、礼仪、司机四个不同的岗位,每个岗位至少有一人参加,且五人均能胜任这四个岗位.
(i)若每人不准兼职,则不同的分配方案有几种?
(ii)若甲乙被抽调去别的地方,剩下三人要求每人必兼两职,则不同的分配方案有几种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com