
【题目】已知函数y=f(x),若在定义域内存在x0 , 使得f(﹣x0)=﹣f(x0)成立,则称x0为函数f(x)的局部对称点.
(1)若a∈R,a≠0,证明:函数f(x)=ax2+x﹣a必有局部对称点;
(2)若函数f(x)=2x+b在区间[﹣1,1]内有局部对称点,求实数b的取值范围;
(3)若函数f(x)=4x﹣m2x+1+m2﹣3在R上有局部对称点,求实数m的取值范围.
【答案】
(1)证明:∵f(x)=ax2+x﹣a,∴f(﹣x)=ax2﹣x﹣a,
令f(﹣x)=﹣f(x)得ax2﹣x﹣a=﹣ax2﹣x+a,化简得ax2﹣a=0(a≠0),
∵△=4a2>0恒成立,
∴方程f(﹣x)=﹣f(x)必定有解,即函数f(x)=ax2+x﹣a必有局部对称点.
(2)解:f(x)=2x+b,f(﹣x)=2﹣x+b,
令f(﹣x)=﹣f(x)得2x+2﹣x=﹣2b,即b=﹣ ![]() (2x+2﹣x),
(2x+2﹣x),
令2x=t,g(t)=﹣ ![]() (t+
(t+ ![]() ),∵x∈[﹣1,1],∴
),∵x∈[﹣1,1],∴ ![]() ,
,
∴g′(t)=﹣ ![]() +
+ ![]() ,令g′(t)=0得t=1或t=﹣1(舍).
,令g′(t)=0得t=1或t=﹣1(舍).
当 ![]() ≤t<1时,g′(t)>0,当1<t≤2时,g′(t)<0,
≤t<1时,g′(t)>0,当1<t≤2时,g′(t)<0,
∴g(t)在[ ![]() ,1]上单调递增,在(1,2]单调递减,
,1]上单调递增,在(1,2]单调递减,
∵g( ![]() )=﹣
)=﹣ ![]() ,g(1)=﹣1,g(2)=﹣
,g(1)=﹣1,g(2)=﹣ ![]() ,
,
∴g(t)的最大值为﹣1,g(t)的最小值为﹣ ![]() .
.
∴b的取值范围是 ![]() .
.
(3)解:f(x)=4x﹣m2x+1+m2﹣3,f(﹣x)=4﹣x﹣m2﹣x+1+m2﹣3,
令f(﹣x)=﹣f(x)得4x+4﹣x﹣2m(2x+2﹣x)+2(m2﹣3)=0(*),
∵f(x)=4x﹣m2x+1+m2﹣3在R上有局部对称点,
∴4x+4﹣x﹣2m(2x+2﹣x)+2(m2﹣3)=0在R上有解.
令2x+2﹣x=t,则t∈[2,+∞),4x+4﹣x=t2﹣2,
∴关于t的方程t2﹣2mt+2m2﹣8=0在t∈[2,+∞)上有解,
令h(t)=t2﹣2mt+2m2﹣8,则h(2)=2m2﹣4m﹣4≤0或  .
.
解得: ![]() 或
或 ![]() ,即1﹣
,即1﹣ ![]() ≤m≤2
≤m≤2 ![]() .
.
∴m的取值范围是[1﹣ ![]() ,2
,2 ![]() ].
].
【解析】(1)令f(﹣x)=﹣f(x)得出关于x的方程,根据判别式证明方程有解即可;(2)令f(﹣x)=﹣f(x)得出关于x的方程,令t=2x得出b关于t的函数g(t),求出函数g(t)在[ ![]() ,2]上的值域即可;(3)令f(﹣x)=﹣f(x)得出关于x的方程,令2x+2﹣x=t得出关于t的一元二次方程在[2,+∞)上有解,根据二次函数的性质不等式方程组求出m的范围.
,2]上的值域即可;(3)令f(﹣x)=﹣f(x)得出关于x的方程,令2x+2﹣x=t得出关于t的一元二次方程在[2,+∞)上有解,根据二次函数的性质不等式方程组求出m的范围.


科目:高中数学 来源: 题型:
【题目】如表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据,根据表提供的数据,求出y关于x的线性回归方程为 ![]() =0.7x+0.35,则下列结论错误的是( )
=0.7x+0.35,则下列结论错误的是( )
x | 3 | 4 | 5 | 6 |
y | 2.5 | t | 4 | 4.5 |
A.产品的生产能耗与产量呈正相关
B.t的取值必定是3.15
C.回归直线一定过点(4,5,3,5)
D.A产品每多生产1吨,则相应的生产能耗约增加0.7吨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某矿山企业生产某产品的年固定成本为![]() 万元,每生产千件该产品需另投入
万元,每生产千件该产品需另投入![]() 万元,设该企业年内共生产此种产品
万元,设该企业年内共生产此种产品![]() 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为![]() 万元,且
万元,且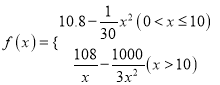
(Ⅰ)写出年利润![]() (万元)关于产品年产量
(万元)关于产品年产量![]() (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)问:年产量![]() 为多少千件时,该企业生产此产品所获年利润最大?
为多少千件时,该企业生产此产品所获年利润最大?
注:年利润=年销售收入-年总成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+)(A>0,ω>0,||<π),在同一周期内,当 ![]() 时,f(x)取得最大值3;当
时,f(x)取得最大值3;当 ![]() 时,f(x)取得最小值﹣3.
时,f(x)取得最小值﹣3.
(1)求函数f(x)的解析式和图象的对称中心;
(2)若 ![]() 时,关于x的方程2f(x)+1﹣m=0有且仅有一个实数解,求实数m的取值范围.
时,关于x的方程2f(x)+1﹣m=0有且仅有一个实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙两人每次射击命中目标的概率分别为 ![]() ,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题中
① 非零向量![]() 满足
满足![]() ,则
,则![]() 的夹角为
的夹角为![]() ;
;
② ![]()
![]() >0是
>0是![]() 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
③若![]() 则
则![]() 必定是直角三角形;
必定是直角三角形;
④△ABC的外接圆的圆心为O,半径为1,若![]() ,且
,且![]() ,则向量
,则向量![]() 在向量
在向量![]() 方向上的投影为
方向上的投影为![]() .
.
以上命题正确的是 __________ (注:把你认为正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲乙丙三辆汽车在不同速度下的燃油效率情况,下列叙述中正确的是( )
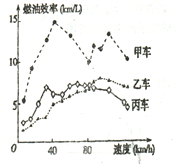
A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比乙车更省油.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com