设函数
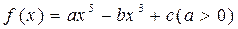
.
(1)若
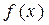
在
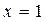
和
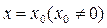
处有不同的极值,且极大值为4,
极小值为1,求
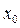
及实数
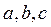
的值;
(2) 若
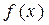
在
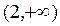
上单调递增且
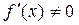
,求
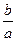
的最大值.
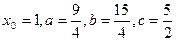
,
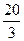
解:(1)
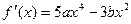
,依题意得:
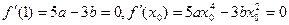
又
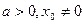
,则
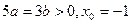
,
所以当
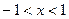
时,
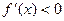
;当
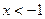
或
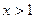
时,
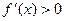
,
故
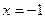
时函数有极大值,
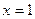
时函数有极小值;
则
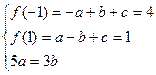
得
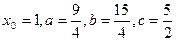
(2)
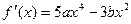
,因为
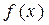
在
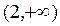
上单调递增,且
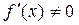
,所以
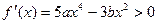
在
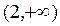
上恒成立。
即
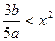
在
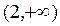
上恒成立,所以
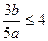
,即
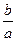
的最大值为
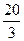
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分13分)
设函数
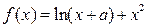
(I)若当
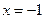
时,
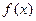
取得极值,求
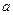
的值,并讨论
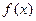
的单调性;
(II)若
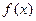
存在极值,求
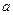
的取值范围,并证明所有极值之和大于
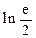
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
函数
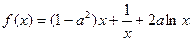
.
(Ⅰ)当
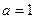
时,求
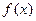
的最小值;
(Ⅱ)当
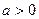
时,求
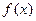
的单调区间.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数
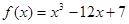
在
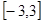
上的最大值与最小值的差是
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
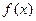
=
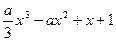
.
(1)若
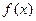
在(-∞,+∞)上是增函数,求a的取值范围.
(2) 若
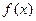
在x=x
1及x=x
2 (x
1, x
2>0)处有极值,且1<
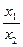
≤5,求a的取值范围。12分
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数
f(
x)=
x3-3
bx+3
b在(0,1)内有极小值,则 ( )
| A.0<b<1 | B.b<1 | C.b>0 | D.b<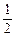 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数
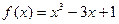
在闭区间
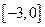
上的最大值,最小值分别是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
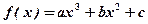
,其导函数图象如图1所示,
则函数
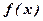
的极小值是 ( * )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数
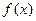
的定义域为区间
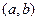
,导函数
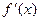
在
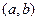
内的图象如图所示,则
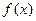
在
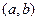
内的极小值点有 ( )
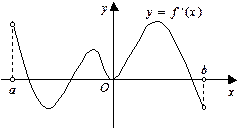
查看答案和解析>>

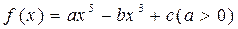 .
. 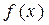 在
在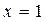 和
和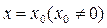 处有不同的极值,且极大值为4,
处有不同的极值,且极大值为4,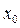 及实数
及实数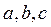 的值;
的值;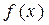 在
在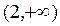 上单调递增且
上单调递增且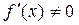 ,求
,求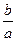 的最大值.
的最大值.  阅读快车系列答案
阅读快车系列答案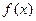 =
=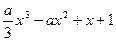 .
.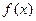 在(-∞,+∞)上是增函数,求a的取值范围.
在(-∞,+∞)上是增函数,求a的取值范围.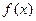 在x=x1及x=x2 (x1, x2>0)处有极值,且1<
在x=x1及x=x2 (x1, x2>0)处有极值,且1<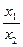 ≤5,求a的取值范围。12分
≤5,求a的取值范围。12分