
【题目】已知函数f(x)= ![]() .
.
( I)判断f(x)的奇偶性;
( II)求证:f(x)+f( ![]() )为定值;
)为定值;
(III)求 ![]() +
+ ![]() +
+ ![]() +f(1)+f(2015)+f(2016)+f(2017)的值.
+f(1)+f(2015)+f(2016)+f(2017)的值.
【答案】解:(I)∵函数f(x)= ![]() .
.
∴函数f(x)= ![]() 的定义域R,定义域关于原点对称.
的定义域R,定义域关于原点对称.
又 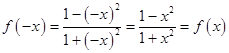 ,
,
∴f(x)是偶函数.…(4分)
证明:(Ⅱ)∵ 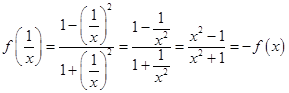 ,
,
∴ ![]() 为定值.
为定值.
解:(Ⅲ)由(II)知 ![]() ,
,![]() +
+ ![]() +
+ ![]() +f(1)+f(2015)+f(2016)+f(2017)
+f(1)+f(2015)+f(2016)+f(2017)
= ![]()
=0+f(1)=0.
【解析】(I)先求出函数f(x)的定义域关于原点对称,再由f(﹣x)=f(x),得到f(x)是偶函数.(Ⅱ)推导出f( ![]() )=﹣f(x),由此能证明
)=﹣f(x),由此能证明 ![]() 为定值.(Ⅲ)由
为定值.(Ⅲ)由 ![]() ,能求出
,能求出 ![]() +
+ ![]() +
+ ![]() +f(1)+f(2015)+f(2016)+f(2017)的值.
+f(1)+f(2015)+f(2016)+f(2017)的值.
【考点精析】解答此题的关键在于理解函数的奇偶性的相关知识,掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称,以及对函数的值的理解,了解函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】f'(x)是函数f(x)的导函数,f'(x)是函数f'(x)的导函数.对于三次函数y=f(x),若方程f'(x0)=0,则点( ![]() )即为函数y=f(x)图象的对称中心.设函数f(x)=
)即为函数y=f(x)图象的对称中心.设函数f(x)= ![]() ,则f(
,则f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )=( )
)=( )
A.1008
B.2014
C.2015
D.2016
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C1: ![]() .
.
(1)求与双曲线C1有相同焦点,且过点P(4, ![]() )的双曲线C2的标准方程;
)的双曲线C2的标准方程;
(2)直线l:y=x+m分别交双曲线C1的两条渐近线于A、B两点.当 ![]()
![]() =3时,求实数m的值.
=3时,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集为实数集R,集合A={x|y= ![]() +
+ ![]() },B={x|2x>4}
},B={x|2x>4}
( I)分别求A∪B,A∩B,(UB)∪A
( II)已知集合C={x|1<x<a},若CA,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() (ax﹣a﹣x)(a>0且a≠1).
(ax﹣a﹣x)(a>0且a≠1).
(1)判断f(x)的奇偶性.
(2)讨论f(x)的单调性.
(3)当x∈[﹣1,1]时,f(x)≥b恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆的参数方程为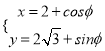 (
(![]() 为参数),以直角坐标系的原点为极点,
为参数),以直角坐标系的原点为极点, ![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)将圆的参数方程化为普通方程,再化为极坐标方程;
(Ⅱ)若点![]() 在直线
在直线![]() 上,当点
上,当点![]() 到圆的距离最小时,求点
到圆的距离最小时,求点![]() 的极坐标.
的极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com