
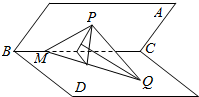
 如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )
如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )| A. | $\frac{2}{3}\sqrt{6}$ | B. | $\frac{3}{4}\sqrt{6}$ | C. | $\frac{4}{3}\sqrt{2}$ | D. | $\frac{3}{2}\sqrt{2}$ |
分析 可作出图形,可设E为P在平面BCD内的射影,并过P作PF⊥BC于F,连接EF,PE,可说明∠PFE=45°,可设PE=m,从而可以得到ME=$\sqrt{2}m$,根据PM=$\sqrt{2}$便可求出m=$\frac{\sqrt{6}}{3}$.可说明∠PQE=30°,从而在RtPQE中可以求出PQ的长度.
解答 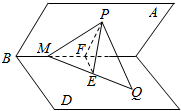 解:如图,设P在平面BCD内的射影为E,过P作PF⊥BC,交BC于F,连接EF,PE;
解:如图,设P在平面BCD内的射影为E,过P作PF⊥BC,交BC于F,连接EF,PE;
∵PE⊥平面BCD,BC?平面BCD;
∴PE⊥BC,即BC⊥PE;
又BC⊥PF,PE∩PF=P;
∴BC⊥平面PEF;
∴BC⊥EF;
∴∠PFE为二面角A-BC-D的平面角,即∠PFE=45°;
设PE=m,则EF=m;
在Rt△FME中,∠FME=45°,∠MFE=90°,则:ME=$\sqrt{2}m$;
在Rt△PME中,PM=$\sqrt{2}$,∠PEM=90°,则:m2+2m2=2;
∴$m=\frac{\sqrt{6}}{3}$;
PE⊥平面BCD,则∠PQE为PQ和平面BCD所成角;
∴∠PQE=30°,又∠PEQ=90°,PE=$\frac{\sqrt{6}}{3}$
∴$PQ=\frac{PE}{sin30°}=\frac{\frac{\sqrt{6}}{3}}{\frac{1}{2}}=\frac{2\sqrt{6}}{3}$.
故选:A.
点评 考查线面垂直的性质及线面垂直的判定定理,二面角的平面角的概念,线面角的概念,以及点在一个平面上的射影的定义,直角三角形的边角关系.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
 如图是一个机器零件的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该机器零件的体积为( )
如图是一个机器零件的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该机器零件的体积为( )| A. | 2+3π+4$\sqrt{2}$ | B. | 2+π | C. | 4+π | D. | 4+2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=1,n=1 | B. | m=4,n=1 | C. | m=3,n=4 | D. | m=4,n=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com