Question

13．椭圆C₁的中心在坐标原点，两焦点分别为双曲线C₂：$\frac{{x}^{2}}{2}$-y²=1的顶点，直x+$\sqrt{2}$y=0与椭圆C₁交于A、B两点，且点A的坐标为（-$\sqrt{2}$，1），点P是椭圆C₁上异于点A，B的任意一点．
（1）求椭圆C₁的标准方程；
（2）求△ABP面积的最大值及此时点P的坐标．

Answer 1

分析 （1）求出椭圆的焦点，结合A（-$\sqrt{2}$，1）在椭圆上，利用椭圆的定义，可得椭圆C₁的方程；
（2）由题意求出B的坐标，设出与AB平行的直线方程，与椭圆方程联立，化为关于x的一元二次方程，利用判别式等于0求出椭圆的切线方程，得到P的坐标，求出|AB|，由平行线间的距离公式求出P到直线AB的距离，代入三角形面积公式得答案．

解答 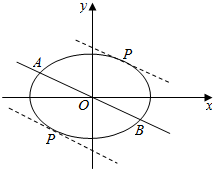解：（1）双曲线C₂：$\frac{{x}^{2}}{2}$-y²=1的顶点为F₁（-$\sqrt{2}$，0），F₂（$\sqrt{2}$，0），
∴椭圆C₁的焦点为F₁（-$\sqrt{2}$，0），F₂（$\sqrt{2}$，0），
∵椭圆过A（-$\sqrt{2}$，1），
∴2a=|AF₁|+|AF₂|=$\sqrt{（-\sqrt{2}+\sqrt{2}）^{2}+（1-0）^{2}}$$+\sqrt{（-\sqrt{2}-\sqrt{2}）^{2}+（1-0）^{2}}$=4，
∴a=2，
∴b=$\sqrt{4-2}=\sqrt{2}$．
则椭圆C₁的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$；
（2）由题意，B（$\sqrt{2}$，-1），如图，
设与直线x+$\sqrt{2}$y=0平行的直线方程为$x+\sqrt{2}y+m=0$．
联立$\left\{\begin{array}{l}{x+\sqrt{2}y+m=0}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$，消去y得：2x²+2mx+m²-4=0．
由△=4m²-8（m²-4）=0，解得m=$±2\sqrt{2}$．
∴与直线x+$\sqrt{2}$y=0平行且与椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$相切的直线方程为$x+\sqrt{2}y±2\sqrt{2}=0$．
此时切点P的坐标为P（$-\sqrt{2}，-1$）、P（$\sqrt{2}，1$）．
|AB|=$\sqrt{（-\sqrt{2}-\sqrt{2}）^{2}+（1+1）^{2}}=2\sqrt{3}$．
P到直线AB的距离d=$\frac{|2\sqrt{2}|}{\sqrt{3}}=\frac{2\sqrt{6}}{3}$．
∴△ABP面积的最大值S=$\frac{1}{2}×2\sqrt{3}×\frac{2\sqrt{6}}{3}=2\sqrt{2}$．

点评 本题考查椭圆的方程，考查直线与椭圆的位置关系，考查三角形面积的计算，考查学生分析解决问题的能力，有难度