
【题目】已知椭圆 C: ![]() =1( a>b>0)经过点 (1,
=1( a>b>0)经过点 (1, ![]() ),离心率为
),离心率为 ![]() ,点 A 为椭圆 C 的右顶点,直线 l 与椭圆相交于不同于点 A 的两个点P (x1 , y1),Q (x2 , y2).
,点 A 为椭圆 C 的右顶点,直线 l 与椭圆相交于不同于点 A 的两个点P (x1 , y1),Q (x2 , y2).
(Ⅰ)求椭圆 C 的标准方程;
(Ⅱ)当 ![]()
![]() =0 时,求△OPQ 面积的最大值;
=0 时,求△OPQ 面积的最大值;
(Ⅲ)若直线 l 的斜率为 2,求证:△APQ 的外接圆恒过一个异于点 A 的定点.
【答案】解:(Ⅰ)由椭圆的离心率e= ![]() =
= ![]() ,即c2=
,即c2= ![]() a2 , 即b2=a2﹣c2=
a2 , 即b2=a2﹣c2= ![]() a2 , a2=4b2 ,
a2 , a2=4b2 ,
将点 (1, ![]() )代入椭圆方程
)代入椭圆方程 ![]() ,即
,即 ![]() ,解得:b2=1,
,解得:b2=1,
∴a2=4,
∴椭圆的标准方程: ![]() ;
;
(Ⅱ)当直线l的斜率不存在时,设l:x=m,代入椭圆方程 ![]() ,
,
P(m, ![]() ),Q(m,﹣
),Q(m,﹣ ![]() ),
),
由 ![]()
![]() =0,(m﹣2)2﹣(1﹣
=0,(m﹣2)2﹣(1﹣ ![]() )=0,解得:m=
)=0,解得:m= ![]() ,m=2(舍去),
,m=2(舍去),
此时丨PQ丨= ![]() ,△OPQ的面积为
,△OPQ的面积为 ![]() ,
,
当直线l的斜率存在时,设l:y=kx+m,代入椭圆方程,(4k2+1)x2+8kmx+4(m2﹣1)=0,
由△>0,则4k2﹣m2+1>0,
x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
由 ![]()
![]() =0,
=0,
(x1﹣2)(x2﹣2)+y1y2=(k2+1)x1x2+(km﹣2)(x1+x2)+m2+4=0,
代入求得12k2+5m2+16km=0,
即m=﹣ ![]() k,m=﹣2k,(此时直线l过点A,舍去),
k,m=﹣2k,(此时直线l过点A,舍去),
丨PQ丨= ![]()
![]() =
= ![]()
![]() ,
,
点O到直线l的距离d= ![]() ,
,
△OPQ的面积为 ![]() ,将m=﹣
,将m=﹣ ![]() k代入,
k代入,![]() ×
×  <
< ![]() ,
,
△OPQ 面积的最大值 ![]() ;
;
(Ⅲ)证明:设直线y=2x+m,代入椭圆方程,整理得:17x2+16mx+4(m2﹣1)=0,
设△△APQ的外接圆方程x2+y2+Dx+Ey+F=0,
联立直线l的方程,5x2+(4m+D+2E)x+(m2+mE+F)=0,
代入可知 ![]() =
= ![]() =
= ![]() ,
,
由外接圆过点A(2,0),则2D+F=﹣4,
从而可得关于D,E,F的三元一次方程组, ,解得:
,解得:  ,
,
代入椭圆方程,整理得:(x2+y2﹣ ![]() x+
x+ ![]() y﹣
y﹣ ![]() )+
)+ ![]() (2x+y﹣4)=0,
(2x+y﹣4)=0,
∴  ,解得:
,解得:  ,或
,或 ![]() ,
,
△APQ 的外接圆恒过一个异于点A的定点( ![]() ,
, ![]() )
)
【解析】(Ⅰ)由椭圆的离心率,求得a和b的关系,将P代入椭圆方程,即可求得a和b的值,求得椭圆方程;(Ⅱ)当斜率不存在时,求P和Q点坐标,由 ![]()
![]() =0,求得m的值,求得丨PQ丨求得,△OPQ的面积,当斜率存在时,设直线l方程,代入椭圆方程,利用韦达定理及弦长公式及三角形的面积公式,即可求得△OPQ 面积的最大值;(Ⅲ)设直线y=2x+m,代入椭圆方程,设外接圆的方程,联立直线l的方程,将A代入外接圆方程,联立方程,即可求得△APQ 的外接圆恒过一个异于点 A 的定点.
=0,求得m的值,求得丨PQ丨求得,△OPQ的面积,当斜率存在时,设直线l方程,代入椭圆方程,利用韦达定理及弦长公式及三角形的面积公式,即可求得△OPQ 面积的最大值;(Ⅲ)设直线y=2x+m,代入椭圆方程,设外接圆的方程,联立直线l的方程,将A代入外接圆方程,联立方程,即可求得△APQ 的外接圆恒过一个异于点 A 的定点.
【考点精析】通过灵活运用椭圆的标准方程,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinxcosx+cos2x
sinxcosx+cos2x
(I)求函数f(x)的最小正周期;
(II)若﹣ ![]() <α<0,f(α)=
<α<0,f(α)= ![]() ,求sin2α的值.
,求sin2α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.
(Ⅰ)求证:BE=DE;
(Ⅱ)若AB=2 ![]() ,AE=3
,AE=3 ![]() ,平面EBD⊥平面ABCD,直线AE与平面ABD所成的角为45°,求二面角B﹣AE﹣D的余弦值.
,平面EBD⊥平面ABCD,直线AE与平面ABD所成的角为45°,求二面角B﹣AE﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a3=5,a5+a6=20,且2 ![]() ,2
,2 ![]() ,2
,2 ![]() 成等比数列,数列{bn}满足bn=an﹣(﹣1)nn.
成等比数列,数列{bn}满足bn=an﹣(﹣1)nn.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)设sn是数列{bn}前n项和,求sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,由直线x=a,x=a+1(a>0),y=x2及 x 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即 a2< ![]() x2dx<(a+1)2 . 类比之,若对n∈N*,不等式
x2dx<(a+1)2 . 类比之,若对n∈N*,不等式 ![]() <A<
<A< ![]() +
+ ![]() +…+
+…+ ![]() 恒成立,则实数A等于( )
恒成立,则实数A等于( ) 
A.ln ![]()
B.ln 2
C.![]() ln 2
ln 2
D.![]() ln 5
ln 5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinωx cosωx﹣sin2ωx+1(ω>0)相邻两条对称轴之间的距离为
sinωx cosωx﹣sin2ωx+1(ω>0)相邻两条对称轴之间的距离为 ![]() .
.
(Ⅰ)求ω的值及函数f(x)的单调递减区间;
(Ⅱ)已知a,b,c分别为△ABC中角A,B,C的对边,且满足a= ![]() ,f(A)=1,求△ABC 面积 S 的最大值.
,f(A)=1,求△ABC 面积 S 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex﹣1﹣a(x+lnx),a∈R.
(1)若曲线y=f(x)在点(1,f(1))处的切线为x轴,求a的值:
(2)在(1)的条件下,求f(x)的单调区间;
(3)若x>0,f(x)≥f(m)恒成立,且f(m)≥0,求证:f(m)≥2(m2﹣m3).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一袋中有7个大小相同的小球,其中有2个红球,3个黄球,2个蓝球,从中任取3个小球.
(I)求红、黄、蓝三种颜色的小球各取1个的概率;
(II)设X表示取到的蓝色小球的个数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程ρ=2cosθ,直线l的参数方程是 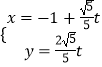 (t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)设直线l与y轴的交点是M,N是曲线C上一动点,求|MN|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com