
【题目】某小学为了解本校某年级女生的身高情况,从本校该年级的学生中随机选出100名女生并统计她们的身高(单位: ![]() ),得到如图频率分布表:
),得到如图频率分布表:
分组(身高) |
|
|
|
|
(Ⅰ)用分层抽样的方法从身高在![]() 和
和![]() 的女生中共抽取6人,则身高在
的女生中共抽取6人,则身高在![]() 的女生应抽取几人?
的女生应抽取几人?
(Ⅱ)在(Ⅰ)中抽取的6人中,再随机抽取2人,求这2人身高都在![]() 内的概率.
内的概率.
【答案】(Ⅰ)4(Ⅱ)![]()
【解析】试题分析: (Ⅰ)根据分层抽样按比例抽取即可; (Ⅱ)在(Ⅰ)中抽取的6名女生中,有4人身高在![]() 中,2人身高在
中,2人身高在![]() 中,从这6人中随机抽取2人,基本事件共有15个, 其中2人身高都在
中,从这6人中随机抽取2人,基本事件共有15个, 其中2人身高都在![]() 内的情况有6种,根据古典概型的公式计算即可.
内的情况有6种,根据古典概型的公式计算即可.
试题解析:(Ⅰ)身高在![]() 内的女生应该抽取
内的女生应该抽取![]() 人.
人.
(Ⅱ)在(Ⅰ)中抽取的6名女生中,有4人身高在![]() 中,2人身高在
中,2人身高在![]() 中,记身高在
中,记身高在![]() 中的4人分别为
中的4人分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,身高在
,身高在![]() 中的2人分别为
中的2人分别为![]() ,
, ![]() .从这6人中随机抽取2人,基本事件包含
.从这6人中随机抽取2人,基本事件包含![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共有15个基本事件.
,共有15个基本事件.
其中2人身高都在![]() 内的情况有6种,
内的情况有6种,
则2人身高都在![]() 内的概率为
内的概率为![]() .
.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】假设要抽查某企业生产的某种品牌的袋装牛奶的质量是否达标,现从700袋牛奶中抽取50袋进行检验,利用随机数表抽取样本时,先将700袋牛奶按001,002,…,700进行编号,如果从随机数表第3行第1组开始向右读,最先读到的5袋牛奶的编号是614,593,379,242,203,请你以此方式继续向右读数,随后读出的3袋牛奶的编号是________.(下列摘取了随机数表第1行至第5行)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点O为极点, ![]() 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知过点P(1,1)的直线
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知过点P(1,1)的直线![]() 的参数方程是
的参数方程是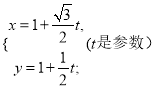
(I)写出直线![]() 的极坐标方程;
的极坐标方程;
(II)设![]() 与圆
与圆![]() 相交于两点A、B,求点P到A、B两点的距离之积
相交于两点A、B,求点P到A、B两点的距离之积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一户居民根据以往的月用电量情况,绘制了月用电量的频率分布直方图(月用电量都在25度到325度之间)如图所示.将月用电量落入该区间的频率作为概率.若每月的用电量在200度以内(含200度),则每度电价0.5元,若每月的用电量超过200度,则超过的部分每度电价0.6元.记![]() (单位:度,
(单位:度,![]() )为该用户下个月的用电量,
)为该用户下个月的用电量,![]() (单位:元)为下个月所缴纳的电费.
(单位:元)为下个月所缴纳的电费.
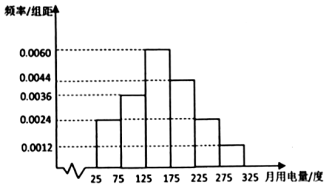
(1)估计该用户的月用电量的平均值(同一组中的数据用该组区间的中点值作代表);
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计下个月所缴纳的电费![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
有甲、乙、丙、丁四名网球运动员,通过对过去战绩的统计,在一场比赛中,甲对乙、丙、丁取胜的概率分别为![]() .
.
(Ⅰ)若甲和乙之间进行三场比赛,求甲恰好胜两场的概率;
(Ⅱ)若四名运动员每两人之间进行一场比赛,设甲获胜场次为![]() ,求随机变量
,求随机变量![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,
, ![]() 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线![]() ,使
,使![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() (
(![]() )的一条直线的两个端点.
)的一条直线的两个端点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() (
(![]() )相交于
)相交于![]() 两点,射线
两点,射线![]() ,
, ![]() 与椭圆
与椭圆![]() 分别相交于点
分别相交于点![]() ,试探究:是否存在数集
,试探究:是否存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() ,使点
,使点![]() 在以线段
在以线段![]() 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com