
分析 (1)通过设公差d、公比q,利用a2=b2+1、a3=b3-2计算可知q=d=3,进而计算可得结论;
(2)通过(1)可知Sn=$\frac{{3}^{n}-1}{2}$,裂项可知cn=$\frac{2}{{3}^{n}-1}$-$\frac{2}{{3}^{n+1}-1}$,并项相加即得结论;
(3)通过(1)可知dn=$\frac{9{n}^{2}-12n+4}{{3}^{n}}$,通过记f(x)=$\frac{9{x}^{2}-12x+4}{{3}^{x}}$并利用导数考查其单调性可知f(x)在区间(-∞,$\frac{2}{3}$)、($\frac{2}{3}+\frac{2}{ln3}$,+∞)上单调递减,在区间($\frac{2}{3}$,$\frac{2}{3}+\frac{2}{ln3}$)上单调递增,进而计算可得结论.
解答 解:(1)依题意,a2=1+d,a3=1+2d,
b2=q(q>0),b3=q2,
∵a2=b2+1,a3=b3-2,
∴1+d=1+q,1+2d=q2-2,
解得:q=d=3或q=d=-1(舍),
∴an=1+3(n-1)=3n-2,bn=3n-1;
(2)由(1)可知Sn=$\frac{1-{3}^{n}}{1-3}$=$\frac{{3}^{n}-1}{2}$,
∴cn=$\frac{{b}_{n+1}}{{S}_{n}•{S}_{n+1}}$=$\frac{{S}_{n+1}-{S}_{n}}{{S}_{n}•{S}_{n+1}}$=$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n+1}}$=$\frac{2}{{3}^{n}-1}$-$\frac{2}{{3}^{n+1}-1}$,
∴数列{cn}的前n项和为$\frac{2}{3-1}$-$\frac{2}{{3}^{2}-1}$+$\frac{2}{{3}^{2}-1}$-$\frac{2}{{3}^{3}-1}$+…+$\frac{2}{{3}^{n}-1}$-$\frac{2}{{3}^{n+1}-1}$=1-$\frac{2}{{3}^{n+1}-1}$=$\frac{{3}^{n+1}-3}{{3}^{n+1}-1}$;
(3)由(1)可知dn=$\frac{{{a}_{n}}^{2}}{{b}_{n+1}}$=$\frac{9{n}^{2}-12n+4}{{3}^{n}}$,
记f(x)=$\frac{9{x}^{2}-12x+4}{{3}^{x}}$,则f′(x)=$\frac{(3x-2)[6-(3x-2)ln3]}{{3}^{x}}$,
令f′(x)=0可知:x=$\frac{2}{3}$或x=$\frac{2}{3}+\frac{2}{ln3}$,
∴当x<$\frac{2}{3}$或x>$\frac{2}{3}+\frac{2}{ln3}$时f′(x)<0,当$\frac{2}{3}$<x<$\frac{2}{3}+\frac{2}{ln3}$时f′(x)>0,
∴f(x)在区间(-∞,$\frac{2}{3}$)、($\frac{2}{3}+\frac{2}{ln3}$,+∞)上单调递减,在区间($\frac{2}{3}$,$\frac{2}{3}+\frac{2}{ln3}$)上单调递增,
∵2<$\frac{2}{3}+\frac{2}{ln3}$<3,f(2)=$\frac{16}{9}$,f(3)=$\frac{49}{27}$,
∴m≥f(3)=$\frac{49}{27}$,
于是实数m的取值范围是[$\frac{49}{27}$,+∞).
点评 本题考查数列的通项及前n项和,考查运算求解能力,涉及利用导数判断函数的单调性,注意解题方法的积累,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
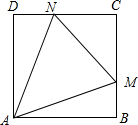 如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )
如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )| A. | 4($\sqrt{2}$-1) | B. | 8($\sqrt{2}$-1) | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=4 | B. | a=6 | C. | a≤6 | D. | a≥6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com