
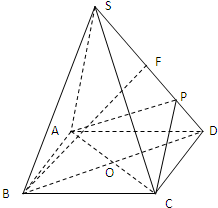
 如图,正四棱锥S-ABCD 的底面是边长为a正方形,O为底面对角线交点,侧棱长是底面边长的
如图,正四棱锥S-ABCD 的底面是边长为a正方形,O为底面对角线交点,侧棱长是底面边长的| 2 |
| SE |
| EC |
| SF |
| FP |
| 2 |
| 1 |
| SE |
| EC |
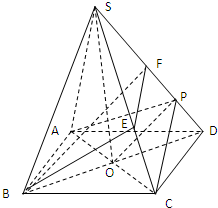 证明:如图,(Ⅰ)连接SO,∵四边形ABCD为正方形,∴AC⊥BD,且 O是平行四边形 ABCD的中心.(1分)
证明:如图,(Ⅰ)连接SO,∵四边形ABCD为正方形,∴AC⊥BD,且 O是平行四边形 ABCD的中心.(1分)| 2 |
| SE |
| EC |
| SF |
| FP |
| 2 |
| 1 |
| SE |
| EC |


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
 如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°.
如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°.查看答案和解析>>
科目:高中数学 来源: 题型:
 12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( )
12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( )查看答案和解析>>
科目:高中数学 来源: 题型:
 (2006•西城区二模)如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的
(2006•西城区二模)如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com