
【题目】已知定义在R上的函数![]() 在[1,2]上有且仅有3个零点,其图象关于点
在[1,2]上有且仅有3个零点,其图象关于点![]() 和直线x
和直线x![]() 对称,给出下列结论:
对称,给出下列结论:
①![]() ;
;
②函数f(x)在[0,1]上有且仅有3个极值点;
③函数f(x)在![]() 上单调递增;
上单调递增;
④函数f(x)的最小正周期是2.
其中所有正确结论的编号是( )
A.②③B.①④C.②③④D.①②
【答案】A
【解析】
先根据条件求得函数的解析式,再结合三角函数的性质判断选项即可.
因为曲线关于点(![]() ,0)对称,所以:
,0)对称,所以:![]() ω+φ=k1π;k1∈Z①
ω+φ=k1π;k1∈Z①
又因为其图象关于直线x![]() 对称,所以:
对称,所以:![]() ω+φ=k2π
ω+φ=k2π![]() ,k2∈Z;②
,k2∈Z;②
由①②可得:ω=[2(k1﹣k2)﹣1]π,即ω=(2n﹣1)π,n∈Z;③
因为![]() 在[1,2]上有且仅有3个零点,
在[1,2]上有且仅有3个零点,
所以![]() 2﹣1
2﹣1![]() ,(ω>0),即2π≤ω<4π,④;
,(ω>0),即2π≤ω<4π,④;
由③④可得ω=3π;
∵f(![]() )=0,∴
)=0,∴![]() φ=kπ,又|φ|
φ=kπ,又|φ|![]() ,∴φ
,∴φ![]() ;
;
∴f(x)=sin(3πx![]() );
);
所以易知f(![]() )
)![]() ;∴①错误;
;∴①错误;
令3πx0![]() kπ,则x0
kπ,则x0![]() ,(k∈Z);令0
,(k∈Z);令0![]() 1,则可取k=0,1,2;∴x0
1,则可取k=0,1,2;∴x0![]() ,
,![]() ,
,![]() ;∴②正确;
;∴②正确;
令![]() 2kπ≤3πx
2kπ≤3πx![]() 2kπ
2kπ![]() k≤x
k≤x![]() k;k∈Z;当k=﹣2时,[
k;k∈Z;当k=﹣2时,[![]() ,
,![]() ]为f(x)的一个递增区间,而(
]为f(x)的一个递增区间,而(![]() ,
,![]() )[
)[![]() ,
,![]() ].∴f(x)在
].∴f(x)在![]() 上单调递增,③正确;
上单调递增,③正确;
∵f(x)=sin(3πx![]() );∴T
);∴T![]() ;④错误.
;④错误.
综上所述,其中正确的结论为②③;
故选:A.


科目:高中数学 来源: 题型:
【题目】设双曲线![]() 的左顶点为D,且以点D为圆心的圆
的左顶点为D,且以点D为圆心的圆![]() 与双曲线C分别相交于点A、B,如图所示.
与双曲线C分别相交于点A、B,如图所示.
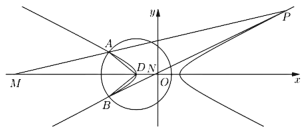
(1)求双曲线C的方程;
(2)求![]() 的最小值,并求出此时圆D的方程;
的最小值,并求出此时圆D的方程;
(3)设点P为双曲线C上异于点A、B的任意一点,且直线PA、PB分别与x轴相交于点M、N,求证:![]() 为定值(其中O为坐标原点).
为定值(其中O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为 (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线![]() 的焦点相同.直线
的焦点相同.直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的一个方向向量为
的一个方向向量为![]() ,求
,求![]() 的面积(其中
的面积(其中![]() 为坐标原点);
为坐标原点);
(3)试问:在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙二人进行一场比赛,该比赛采用三局两胜制,即先获得两局胜利者获得该场比赛胜利.在每一局比赛中,都不会出现平局,甲获胜的概率都为![]() .
.
(1)求甲在第一局失利的情况下,反败为胜的概率;
(2)若![]() ,比赛结束时,设甲获胜局数为
,比赛结束时,设甲获胜局数为![]() ,求其分布列和期望
,求其分布列和期望![]() ;
;
(3)若甲获得该场比赛胜利的概率大于甲每局获胜的概率,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]() ,左顶点为A,过点A的直线l与C交于另一个点M,且与直线x=t交于点N.
,左顶点为A,过点A的直线l与C交于另一个点M,且与直线x=t交于点N.
(1)求椭圆C的方程;
(2)是否存在实数t,使得![]() 为定值?若存在,求实数t的值;若不存在,请说明理由.
为定值?若存在,求实数t的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线![]() 是过点
是过点![]() 的动直线,当
的动直线,当![]() 与圆
与圆![]() 相切时,同时也和抛物线
相切时,同时也和抛物线![]() 相切.
相切.
(1)求抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,与圆
,与圆![]() 交于不同的两点A、B,
交于不同的两点A、B,![]() 面积为
面积为![]() ,
,![]() 面积为
面积为![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单位圆O:x2+y2=1上任取一点P(x,y),圆O与x轴正向的交点是A,设将OA绕原点O旋转到OP所成的角为θ,记x,y关于θ的表达式分别为x=f(θ),y=g(θ),则下列说法正确的是( )
A.x=f(θ)是偶函数,y=g(θ)是奇函数
B.x=f(θ)在![]() 为增函数,y=g(θ)在
为增函数,y=g(θ)在![]() 为减函数
为减函数
C.f(θ)+g(θ)≥1对于![]() 恒成立
恒成立
D.函数t=2f(θ)+g(2θ)的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
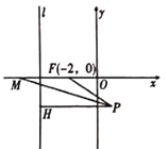
【题目】如图,在平面直角坐标系中,已知点![]() ,直线
,直线![]() ,过动点
,过动点![]() 作
作![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,且
,且![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作两条直线,分别交曲线
作两条直线,分别交曲线![]() 于
于![]() 两点(异于
两点(异于![]() 点).当直线
点).当直线![]() 的斜率之和为2时,直线
的斜率之和为2时,直线![]() 是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com