
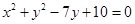 相交,所得公共弦平行于已知直线
相交,所得公共弦平行于已知直线 ,又圆C经过点A(-2,3),B(1,4),求圆C的方程。
,又圆C经过点A(-2,3),B(1,4),求圆C的方程。
 ,
, …………….. 4分
…………….. 4分
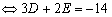 ①又点A、B在圆C上,故有:
①又点A、B在圆C上,故有:  ②
②  ③……………………………… 7分
③……………………………… 7分 ……………………….………..10分
……………………….………..10分 ,
,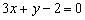 ④
④ 

 ⑤………….6分
⑤………….6分 解之得
解之得 

 ………………………………………………10分
………………………………………………10分

 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源:不详 题型:填空题
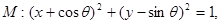 直线
直线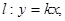 下面四个命题
下面四个命题
 和
和 直线
直线 和圆
和圆 相切
相切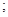
 和
和 直线
直线 和圆
和圆 有公共点
有公共点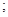
 必存在实数
必存在实数 使得直线
使得直线 和圆
和圆 相切
相切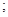
 必存在实数
必存在实数 使得直线
使得直线 和圆
和圆 相切
相切查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.-3<a<7 | B.-6<a<4 |
| C.-7<a<3 | D.-21<a<19 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,点P是椭圆C:
,点P是椭圆C: 上一点,过点P作圆O的两条切线PA、PB,A、B为切点,直线AB分别交
上一点,过点P作圆O的两条切线PA、PB,A、B为切点,直线AB分别交 轴、
轴、 轴于点M、N,则
轴于点M、N,则 的面积的最小值是
的面积的最小值是 B.1 C.
B.1 C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com