
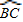 上取一点P,若∠BOP=2θ,把PA+PB+PC表示成θ的函数;
上取一点P,若∠BOP=2θ,把PA+PB+PC表示成θ的函数;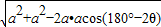 =2acosθ,
=2acosθ,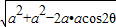 =2asinθ,
=2asinθ,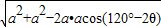 =2asin(60°-θ),
=2asin(60°-θ),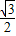 cosθ-
cosθ- sinθ)
sinθ)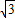 )acosθ.
)acosθ.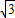 )acosθ=2a
)acosθ=2a 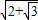 (
(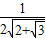 sinθ+
sinθ+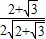 cosθ)
cosθ)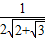 ,sinα=
,sinα= ,则 f(θ)=2a
,则 f(θ)=2a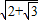 sin(θ+α),
sin(θ+α),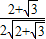 >45°,故 当θ=90°-arcsin
>45°,故 当θ=90°-arcsin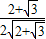 时,sin(θ+α)=1取得最大值,
时,sin(θ+α)=1取得最大值,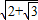 .
.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
 | BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
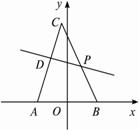
(1)以AB所在直线为x轴,AB中点为坐标原点,建立如图所示的平面直角坐标系,求点P的轨迹方程.
(2)若F、G是点P的轨迹上任意两个不同的点,且线段FG的中垂线与直线AB相交,交点为Q(t,0).
①证明:存在最小的正数M,使得t<M,并求M的值.
②若M=![]() ,求∠APC的取值范围.
,求∠APC的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com