
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD. (Ⅰ)求证:AD⊥平面BFED;
(Ⅱ)在线段EF上是否存在一点P,使得平面PAB与平面ADE所成的锐二面角的余弦值为 ![]() .若存在,求出点P的位置;若不存在,说明理由.
.若存在,求出点P的位置;若不存在,说明理由.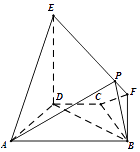
【答案】解:(Ⅰ)在梯形ABCD中, 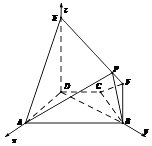
∵AB∥CD,AD=DC=CB=1,∠BCD=120°,
∴故 AB=2,
∴BD2=AB2+AD2﹣2ABADcos60°=3,
∴AB2=AD2+BD2
∴BD⊥AD,
∵平面BFED⊥平面ABCD,平面BFED∩平面ABCD=BD,
∴AD⊥平面BFED.
(Ⅱ)∵AD⊥平面BFED,∴AD⊥DE,
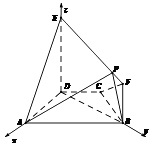
以D为原点,分别以DA,DE,DE为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则D(0,0,0),A(1,0,0),B(0, ![]() ,0),P(0,λ,
,0),P(0,λ, ![]() ),
),![]() =(﹣1,
=(﹣1, ![]() ,0),
,0), ![]() =
= 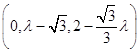 .
.
取平面EAD的一个法向量为 ![]() =(0,1,0),
=(0,1,0),
设平面PAB的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
由 ![]() =0,
=0, ![]()
![]() =0得:
=0得: 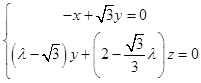 ,取y=1,可得
,取y=1,可得 ![]() =(
=( 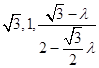 ).
).
∵二面角A﹣PD﹣C为锐二面角,平面PAB与平面ADE所成的锐二面角的余弦值为 ![]() .
.
∴cos< ![]() =
= ![]() =
= 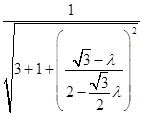 =
= ![]() ,
,
解得λ= ![]() ,即P为线段EF的3等分点靠近点E的位置
,即P为线段EF的3等分点靠近点E的位置
【解析】(Ⅰ)推出AB=2,求解AB2=AD2+BD2 , 证明BD⊥AD,然后证明AD⊥平面BFED.(Ⅱ)以D为原点,分别以DA,DE,DE为x轴,y轴,z轴建立如图所示的空间直角坐标系,求出相关点的坐标,求出平面EAD的一个法向量,平面PAB的一个法向量,利用向量的数量积,转化求解即可.
【考点精析】关于本题考查的直线与平面垂直的判定,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若关于x的不等式xex﹣2ax+a<0的非空解集中无整数解,则实数a的取值范围是( )
A.[ ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() )
)
C.[ ![]() ,e]
,e]
D.[ ![]() ,e]
,e]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果数列![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ,且
,且![]() ),满足:①
),满足:①![]() ,
,![]() ;
;
②![]() ,那么称数列
,那么称数列![]() 为“
为“![]() ”数列.
”数列.
(![]() )已知数列
)已知数列![]() ,
,![]() ,
,![]() ,
,![]() ;数列
;数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .试判断数列
.试判断数列![]() ,
,![]() 是否为“
是否为“![]() ”数列.
”数列.
(![]() )是否存在一个等差数列是“
)是否存在一个等差数列是“![]() ”数列?请证明你的结论.
”数列?请证明你的结论.
(![]() )如果数列
)如果数列![]() 是“
是“![]() ”数列,求证:数列
”数列,求证:数列![]() 中必定存在若干项之和为
中必定存在若干项之和为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式|x﹣3|+|x﹣m|≥2m的解集为R. (Ⅰ)求m的最大值;
(Ⅱ)已知a>0,b>0,c>0,且a+b+c=m,求4a2+9b2+c2的最小值及此时a,b,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲,乙两个抽奖方案供员工选择. 方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率均为 ![]() ,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为 ![]() ,每次中奖均可获得奖金400元.
,每次中奖均可获得奖金400元.
(Ⅰ)求某员工选择方案甲进行抽奖所获奖金X(元)的分布列;
(Ⅱ)试比较某员工选择方案乙与选择方案甲进行抽奖,哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD的中点,PE⊥BE,PA=PD=AD=2,AB=![]() .
.
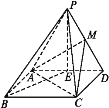
(1)求证:PB∥平面MAC.
(2)求证:平面MAC⊥平面PBE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com