
【题目】设函数![]() .
.
(Ⅰ)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)求函数f(x)单调区间.
【答案】(Ⅰ)x﹣y+1=0.(Ⅱ)当a=0时,单调递增区间是(﹣∞,0),单调递减区间是(0,+∞).当0<a<1时,单调递增区间是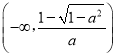 和
和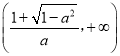 ,单调递减区间是
,单调递减区间是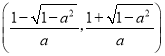 .当a≥1时,单调递增区间是(﹣∞,+∞),无减区间.当﹣1<a<0时,单调递减区间是
.当a≥1时,单调递增区间是(﹣∞,+∞),无减区间.当﹣1<a<0时,单调递减区间是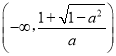 和
和 ,单调递增区间
,单调递增区间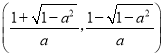 .当a≤﹣1时,单调递减区间是(﹣∞,+∞),无增区间.
.当a≤﹣1时,单调递减区间是(﹣∞,+∞),无增区间.
【解析】
(I)先求导数f'(x),利用导数求出在x=0处的导函数值,即为切线的斜率,则可得出切线方程.
(II)对字母a进行分类讨论,再令f'(x)大于0,解不等式,可得函数的单调增区间,令导数小于0,可得函数的单调减区间.
因为![]() ,所以
,所以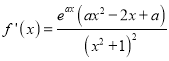 .
.
(Ⅰ)当a=1时,![]() ,
,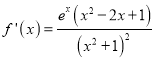 ,
,
所以f(0)=1,f'(0)=1.
所以曲线y=f(x)在点(0,f(0))处的切线方程为x﹣y+1=0.
(Ⅱ)因为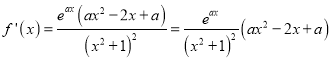 ,
,
(1)当a=0时,由f'(x)>0得x<0;由f'(x)<0得x>0.
所以函数f(x)在区间(﹣∞,0)单调递增,在区间(0,+∞)单调递减.
(2)当a≠0时,设g(x)=ax2﹣2x+a,方程g(x)=ax2﹣2x+a=0的判别式△=4﹣4a2=4(1﹣a)(1+a),
①当0<a<1时,此时△>0.
由f'(x)>0得![]() ,或
,或![]() ;
;
由f'(x)<0得![]() .
.
所以函数f(x)单调递增区间是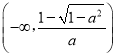 和
和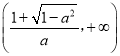 ,
,
单调递减区间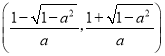 .
.
②当a≥1时,此时△≤0.所以f'(x)≥0,
所以函数f(x)单调递增区间是(﹣∞,+∞).
③当﹣1<a<0时,此时△>0.
由f'(x)>0得![]() ;
;
由f'(x)<0得![]() ,或
,或![]() .
.
所以当﹣1<a<0时,函数f(x)单调递减区间是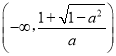 和
和 ,
,
单调递增区间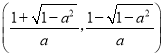 .
.
④当a≤﹣1时,此时△≤0,f'(x)≤0,所以函数f(x)单调递减区间是(﹣∞,+∞).


科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(I)在答题卡上作出这些数据的频率分布直方图:
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
查看答案和解析>>
科目:高中数学 来源: 题型:
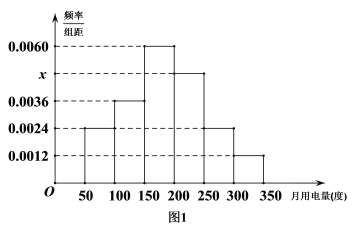
【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图1.
A类用户 | B类用户 | |||||||
9 | 7 | 7 | 0 | 6 | ||||
8 | 6 | 5 | 1 | 7 | 8 | 9 | ||
9 | 8 | 2 | 8 | 5 | 6 | 7 | 8 | |
8 | 7 | 1 | 0 | 9 | 7 | 8 | 9 | |
图2
(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;(2)若将用电量在区间
的值并估计这50户用户的平均用电量;(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图2;若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图2;若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
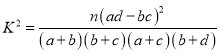 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据茎叶如图所示.
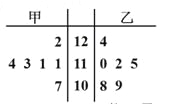
(Ⅰ)根据样本数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对稳定;
(Ⅱ)若从乙车间![]() 件样品中随机抽取两件,求所抽取两件样品重量之差不超过
件样品中随机抽取两件,求所抽取两件样品重量之差不超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如右图所示.经销商为下一个销售季度购进了130t该农产品.以![]() (单位:t,100≤
(单位:t,100≤![]() ≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.

(Ⅰ)将T表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润T不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是两个小区所在地,
是两个小区所在地,![]() 、
、![]() 到一条公路
到一条公路![]() 的垂直距离分别为
的垂直距离分别为![]()
![]() ,
,![]()
![]() ,
,![]() 两端之间的距离为
两端之间的距离为![]()
![]() .
.
(1)某移动公司将在![]() 之间找一点
之间找一点![]() ,在
,在![]() 处建造一个信号塔,使得
处建造一个信号塔,使得![]() 对
对![]() 、
、![]() 的张角与
的张角与![]() 对
对![]() 、
、![]() 的张角相等,试确定点
的张角相等,试确定点![]() 的位置.
的位置.
(2)环保部门将在![]() 之间找一点
之间找一点![]() ,在
,在![]() 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得![]() 对
对![]() 、
、![]() 所张角最大,试确定点
所张角最大,试确定点![]() 的位置.
的位置.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com