
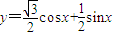 的最小正周期、单调区间、最值及取得最值时对应的x的集合.
的最小正周期、单调区间、最值及取得最值时对应的x的集合. cosx+
cosx+ sinx转化为y=sin(x+
sinx转化为y=sin(x+ ),利用正弦函数的性质即可求得其最小正周、单调区间、最值及取得最值时对应的x的集合.
),利用正弦函数的性质即可求得其最小正周、单调区间、最值及取得最值时对应的x的集合. cosx+
cosx+ sinx=sin(x+
sinx=sin(x+ ),
), ≤x+
≤x+ ≤2kπ+
≤2kπ+ ,k∈Z得2kπ-
,k∈Z得2kπ- ≤x≤2kπ+
≤x≤2kπ+ ,k∈Z,
,k∈Z, cosx+
cosx+ sinx的单调递增区间为[2kπ-
sinx的单调递增区间为[2kπ- ,2kπ+
,2kπ+ ],k∈Z.
],k∈Z. cosx+
cosx+ sinx的单调递减区间为[2kπ+
sinx的单调递减区间为[2kπ+ ,2kπ+
,2kπ+ ],k∈Z.
],k∈Z. =2kπ+
=2kπ+ ,k∈Z得x=2kπ+
,k∈Z得x=2kπ+ ,即当x=2kπ+
,即当x=2kπ+ 时,y=
时,y= cosx+
cosx+ sinx取得最大值1;
sinx取得最大值1; =2kπ-
=2kπ- ,k∈Z得x=2kπ-
,k∈Z得x=2kπ- ,即当x=2kπ-
,即当x=2kπ- 时,y=
时,y= cosx+
cosx+ sinx取得最小值-1;
sinx取得最小值-1; cosx+
cosx+ sinx取得最大值时,相应的x的集合为{x|x=2kπ+
sinx取得最大值时,相应的x的集合为{x|x=2kπ+ ,k∈Z};
,k∈Z}; cosx+
cosx+ sinx取得最小值时,相应的x的集合为{x|x=2kπ-
sinx取得最小值时,相应的x的集合为{x|x=2kπ- ,k∈Z}.
,k∈Z}.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源:2010-2011学年福建省厦门市高三10月月考文科数学试卷 题型:解答题
已知: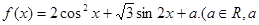 为常数)
为常数)
(1)若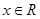 ,求
,求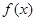 的最小正周期及单调区间;
的最小正周期及单调区间;
(2)若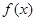 在[
在[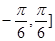 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求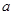 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建师大附中高三上学期期中考试理科数学卷 题型:解答题
(本小题12分)设函数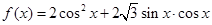 ,
,
(I)求 的最小正周期以及单调增区间;
的最小正周期以及单调增区间;
(II)当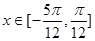 时,求
时,求 的值域;
的值域;
(Ⅲ)若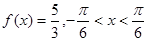 ,求
,求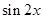 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2012届福建南安侨光中学高三第三次阶段考理科数学试卷 题型:解答题
已知向量 ,设函数
,设函数 。
。
(1)求 的最小正周期与单调递减区间。
的最小正周期与单调递减区间。
(2)在 中,
中, 、
、 、
、 分别是角
分别是角 、
、 、
、 的对边,若
的对边,若 的面积为
的面积为 ,求
,求 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com