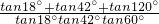练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    数学公式=________．

    -1
    分析：根据60°=18°+42°，由两角和的正切函数公式化简后，得到tan18°+tan42°与tan18°tan42°的关系，然后把所求的式子利用特殊角的三角函数值化简后，将得到的关系式代入，化简后即可求出值．
    解答：由tan60°=tan（18°+42°）==，
    得到tan18°+tan42°=-tan18°tan42°，
    则
    =
    ==-1．
    故答案为：-1
    点评：此题考查学生灵活运用两角和的正切函数公式化简求值，是一道基础题．学生做题时注意角度的变换．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （本题满分8分．老教材试题第1小题4分，第2小题4分；新教材试题第1小题3分，第2小题5分．）
    （老教材）
    设a为实数，方程2x2-8x+a+1=0的一个虚根的模是数学公式．
    （1）求a的值；
    （2）在复数范围内求方程的解．    		（新教材）
    设函数f（x）=2x+p，（p为常数且p∈R）
    （1）若f（3）=5，求f（x）的解析式；
    （2）在满足（1）的条件下，解方程：f-1（x）=2+log2x2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    下列说法中错误的是


    1. A.
      如果变量x与y之间存在着线性相关关系，则我们根据试验数据得到的点（xi，yi）（i=1，2，…，n）将散布在某一条直线的附近
    2. B.
      如果两个变量x与y之间不存在着线性关系，那么根据它们的一组数据（xi，yi）（i=1，2，…，n）不能写出一个线性方程
    3. C.
      设x，y是具有相关关系的两个变量，且x关于y的线性回归方程为数学公式=bx+a，b叫做回归系数
    4. D.
      为使求出的线性回归方程有意义，可用统计检验的方法来判断变量y与x之间是否存在线性相关关系

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    【待处理】已知|a|=10，|b|=12，且（3a）•（数学公式b）=-36，则a与b的夹角是


    1. A.
      60°
    2. B.
      120°
    3. C.
      135°
    4. D.
      150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

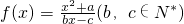    对于函数f（x），若存在x0∈R，使得f（x0）=x0，则称x0为函数f（x）的不动点，若函数数学公式有且仅有两个不动点0和2，且数学公式．
    （1）试求函数f（x）的表达式；
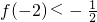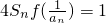    （2）已知各项不为0的数列{an}满足数学公式，其中Sn表示数列{an}的前n项和，求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    四面体ABCD四个面的重心分别为E、F、G、H，则四面体EFGH的表面积与四面体ABCD的表面积的比值是


    1. A.
      数学公式
    2. B.
      数学公式
    3. C.
      数学公式
    4. D.
      数学公式

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    如图，在平面直角坐标系xOy中，椭圆数学公式+数学公式=1（a＞b＞0）被围于由4条直线x=±a，y=±b所围成的矩形ABCD内，任取椭圆上一点P，若数学公式=m•数学公式+n•数学公式（m、n∈R），则m、n满足的一个等式是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知m＞1，且存在x∈[-2，0]，使不等式x2+2mx+m2-m≤0成立，则m的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    函数y=f（x）定义在区间（-3，7）上，其导函数如右图所示，则函数y=f（x）在区间（-3，7）上极小值的个数是________个．

    查看答案和解析>>

    同步练习册答案